Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 95a
A tensão normal admissível para o aço da barra mostrada vale 125 Mpa. Determinar a máxima força P admissível, axial e centrada, que pode ser aplicada a barra sabendo-se que
Passo 1
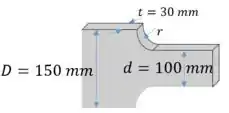
Começamos a questão observando o gráfico de Coeficientes de Concentração de Tensões no livro. Vamos calcular as propriedades necessárias:
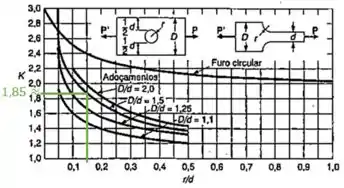
Observando o gráfico, o coeficiente de concentração de tensão será aproximadamente:
Passo 2
Primeiro calculamos a área de seção transversal da parte menor
E calculamos a tensão:
Isolamos o
A força é:
Resposta
Exercícios de Livros Relacionados
O estado de tensões mostrado ocorre em um componente de máquina, que é feito de um latão para o qual σ e = 175M P a . Usando o critério da máxima energia de distorção, determinar se o escoamento ocorr
O estado de tensões mostrado ocorre em um componente de máquina, que é feito de um latão para o qual σ e = 175M P a . Usando o critério da máxima energia de distorção, determinar a variação dos valore
O estado de tensões mostrado ocorre em um componente de máquina, que é feito de um aço para o qual σ e = 415M P a . Usando o critério da máxima energia de distorção, determinar o coeficiente de segura
Usando o método do trabalho e energia, determinar a deflexão em C , provocada pela carga P .
Usando o método do trabalho e energia, determinar a deflexão em C , provocada pela carga P .