Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 156b

Para o carregamento mostrado, determinar:

b) o ponto onde a linha neutra intercepta a linha ABD

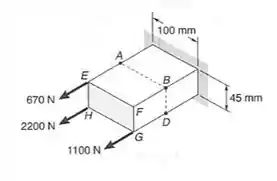
Passo 1

Para determinação de tensões em elementos que estão sujeitos a momentos fletores inclinados, ou ainda, momentos fletores oblíquos, ou momentos fletores assimétricos, temos a seguinte fórmula:

σ = P A - M z y I z z + M y z I y y

Em que:

M z = p a r c e l a   d o   m o m e n t o   n a   d i r e ç ã o   z

M y = p a r c e l a   d o   m o m e n t o   n a   d i r e ç ã o   x

y   e   z = c o o r d e n a d a s   n o   p o n t o   e m   q u e   s e   d e s e j a   s a b e r   a   t e n s ã o   e m   c a d a   d i r e ç ã o

I z z = m o m e n t o   d e   i n é r c i a   e m   t o r n o   d e   z

I y y = m o m e n t o   d e   i n é r c i a   e m   t o r n o   d e   y

Precisamos então definir os carregamentos que agem na nossa seção, para isso precisamos ver a nossa seção, com isso teremos que:

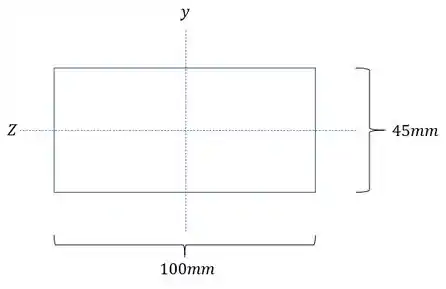
Passo 2

Se temos a seção, podemos pensar os carregamentos que agem, sendo assim podemos pensar o seguinte:

  • Carga P

    • P = 2200 + 1100 + 670 = 3970   N

  • Carga de momento na direção y

    • Para termos os momentos na direção y, precisamos das distancia na direção Z, e com isso podemos analisar as cargas que agem na seção.

    M y = 670   .   50 + 2200   .   50 - 1100   .   50 = 88500   N m m

  • Carga de momento na direção Z

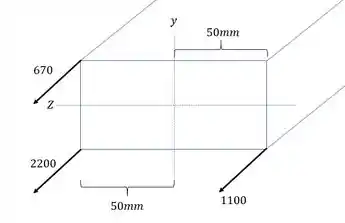
    • Para termos os momentos na direção Z, precisamos das distancia na direção Y, e com isso podemos analisar as cargas que agem na seção.

    M z = - 670   .   22,5 + 2200   .   22,5 + 1100   .   22,5 = 59175   N m m

    Passo 3

    Os dados de seção que podemos analisar são dados por:

    A = 100   .   45 = 4500   m m 2

    I z z = b h 3 12 = 100   .     45 3 12 = 759375   m m 4

    I y y = h b 3 12 = 45   .     100 3 12 = 3750000   m m 4

    Passo 4

    E agora precisamos determinar os valores de y e z de cada ponto que desejamos determinar as tensões, sendo assim, teremos que:

  • Para o ponto A temos que:

  • Para o ponto B temos que:

  • Para o ponto D temos que:

  • Para o ponto C temos que:

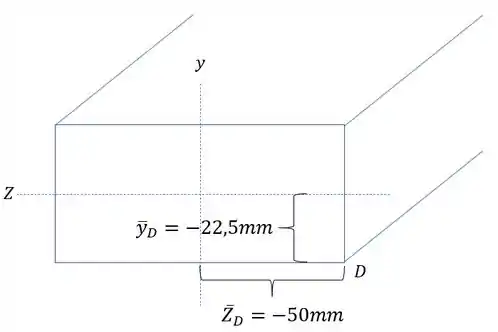
Substituindo a tensão, teremos que:

σ A = P A - M z y A I z z + M y z A I y y

σ A = 3970 4500 - 59175   .     22,5 759375 + 88500   .     50 3750000 = 0,31   M P a = 310   k P a

σ B = P A - M z y B I z z + M y z B I y y

σ B = 3970 4500 - 59175   .     22,5 759375 + 88500   .     - 50 3750000 = - 2,05   M P a = - 2050   k P a

σ C = P A - M z y C I z z + M y z C I y y

σ c = 3970 4500 - 59175   .     - 22,5 759375 + 88500   .     50 3750000 = 3,82     M P a = 3820   k P a

σ D = P A - M z y D I z z + M y z D I y y

σ D = 3970 4500 - 59175   .     - 22,5 759375 + 88500   .     - 50 3750000 = 1,46   M P a = 1456   k P a

Tendo as tensões, podemos anotar elas na nossa seção.

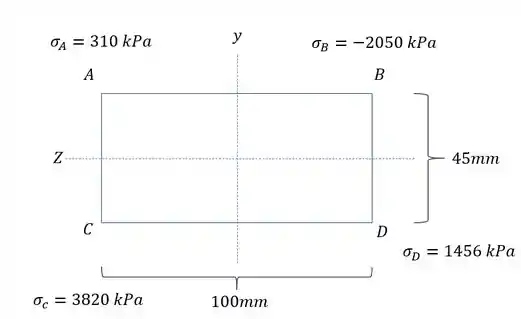
Olhando a face com a reta AB e desenhando o diagrama, teremos que:

Olhando a face com a reta BD e desenhando o diagrama, teremos que:

Assim a LN será:

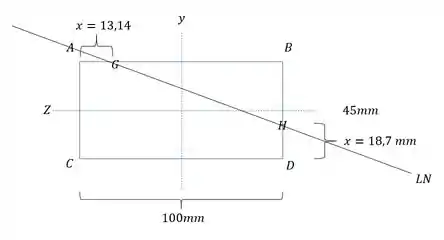
Resposta

c) a LN está a 13,14 mm do ponto A na direção AB e a 18,7 de D na direção BD

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O anel mostrado na figura tem um raio interno r 1 = 20,3m m e uma seção transversal circular de diâmetro d = 15,24m m . Sabendo que cada uma das forças de 534 N é aplicada ao centroide da seção transv
A barra mostrada tem seção transversal circular de 14 mm de diâmetro. Sabendo que a = 32m m , determine a tensão (a) no ponto A, (b) no ponto B.(Obs: o enunciado diz que o tubo tem 14 mm de diâmetro,
Resolva o problema 4.175 considerando que o anel tem um raio interno r 1 = 15,24m m e uma seção transversal circular de diâmetro d = 20,3m m .
Sabendo que a máxima tensão admissível é 45 MPa, determine a intensidade do maior momento M que pode ser aplicado aos componentes mostrados.
A barra mostrada tem seção transversal circular de 14 mm de diâmetro. Sabendo que a tensão admissível é de 38 MPa, determine a maior distância a permitida entre a linha de ação da força de 220 N e o p