Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 178
A barra mostrada tem seção transversal circular de 14 mm de diâmetro. Sabendo que a tensão admissível é de 38 MPa, determine a maior distância permitida entre a linha de ação da força de 220 N e o plano que contém o centro de curvatura dessa barra.
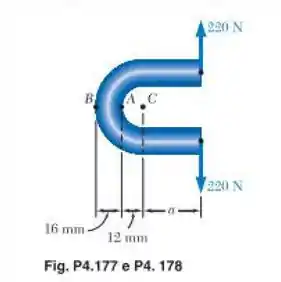
(Obs: o enunciado diz que o tubo tem 14 mm de diâmetro, no entanto no desenho é apontado 16 mm entre A e B, que corresponde ao diâmetro também, vamos considerar esse valor para o diâmetro).
Passo 1
Beleza! Vamos começar esse exercício escrevendo o raio interno da seção, que pode ser visto através da figura do enunciado, então temos:
Agora, para o raio externo da seção, que será dado pelo raio interno mais o diâmetro da seção, teremos:
Agora vamos escrever o raio médio da seção, que será dado por:
Agora vamos calcular a área da seção, então temos:
Agora, para encontrar a localização do raio da superfície neutra da seção, vamos recorrer a fórmula para o círculo apresentada na figura 4.61 dessa seção, onde temos:
Em que é o raio da seção. Então substituindo os valores conhecidos nessa equação, temos:
Passo 2
Agora podemos encontrar a excentricidade da seção, que é a distância entre a linha neutra e o centroide da seção, através de:
Substituindo os valores conhecidos, teremos:
Agora, precisamos escrever o momento gerado pela força de 220 N aplicada na seção, nesse caso ficou fácil ver que o binário vai ser o braço de alavanca , que vai do ponto de aplicação da força até o centroide da seção transversal, multiplicado pela força de 220 N, então teremos:
Passo 3
Para encontrar a maior distância admissível, vamos utilizar a equação 4,71 vista nesse capítulo, lembrando que agora também temos a força de tração que deve ser somada a parcela de tensão gerada pelo momento. Como já passamos pelo exercício 4.177, sabemos que a maior tensão ocorre no ponto A, então só precisamos calcular a máxima distância permitida levando esse ponto em consideração. Dessa forma, a equação 4.71 se torna:
Substituindo a expressão para o momento, chegamos em:
Agora nós vamos manipular essa equação para isolar o , vamos lá:
Substituindo os valores conhecidos, teremos: