Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 69
Uma mola é feita de um arame circular de raio c, formando uma hélice de raio R. Determinar a máxima tensão de cisalhamento produzida pelas forças P e P’, iguais e opostas. (Sugestão: Determinar inicialmente a força cortante V e o torque T, em uma seção transversal.)
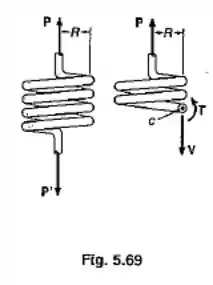
Passo 1
Fazendo uma análise das forças temos
Passo 2
Por conta de T teremos então
Por conta da força V teremos
Passo 3
Por superposição temos
Resposta
Exercícios de Livros Relacionados
A viga mostrada na figura suporta uma carga distribuída uniforme w. Se for feita de uma chapa com largura constante b, determine a tensão de flexão máxima absoluta na viga.
As polias acopladas ao eixo estão carregadas como mostra a figura. Se os mancais em A e B exercem somente forças horizontais e verticais sobre o eixo, determine, com aproximação de 1m m , o diâmetro e
Os mancais em A e D exercem somente as componentes y e z da força sobre o eixo. Se τ a d m = 60M P a , determine, com aproximação de 1m m , o eixo de menor diâmetro que suportará a carga. Use a teoria
Os mancais em A e D exercem somente as componentes y e z da força sobre o eixo. Se τ a d m = 60 MPa, determine, com aproximação de 1 mm, o eixo de menor diâmetro que suportará a carga. Use a teoria da
Os mancais em A e D exercem somente as componentes y e z da força sobre o eixo. Se τ a d m = 60M P a , determine, com aproximação de 1m m , o eixo de menor diâmetro que suportará a carga. Use a teoria