Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 175

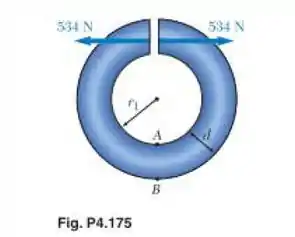
O anel mostrado na figura tem um raio interno r 1 = 20,3   m m e uma seção transversal circular de diâmetro d = 15,24   m m . Sabendo que cada uma das forças de 534 N é aplicada ao centroide da seção transversal, determine a tensão no (a) ponto A e (b) ponto B.

Passo 1

Beleza! Vamos começar esse exercício escrevendo o raio externo da seção, que será dado pelo raio interno mais o diâmetro, então teremos:

r 2 = r 1 + d = 20,3 + 15,24 → r 2 = 35,54   m m = 0,03554   m

Agora vamos escrever o raio médio da seção, que será dado por:

r - = 1 2 r 1 + r 2 = 1 2 20,3 + 35,54 → r - = 27,92   m m = 0,02792   m

Agora vamos calcular a área da seção, então temos:

A = π d 2 4 = π 0,01524 2 4 → A = 182,41.10 - 6   m 2

Agora, para encontrar a localização do raio da superfície neutra da seção, vamos recorrer a fórmula para o círculo apresentada na figura 4.61 dessa seção, onde temos:

R = 1 2 r - + r - 2 - c 2

Em que c é o raio da seção. Então substituindo os valores conhecidos nessa equação, temos:

R = 1 2 0,02792 + 0,02792 2 - 0,00762 2 → R = 27,39.10 - 3   m

Passo 2

Agora podemos encontrar a excentricidade e da seção, que é a distância entre a linha neutra e o centroide da seção, através de:

e = r - - R

Substituindo os valores conhecidos, teremos:

e = 0,02792 - 27,39.10 - 3 → e = 0,53.10 - 3   m

Agora precisamos encontrar o momento que será aplicado a seção em função do carregamento dado e a força interna de reação gerada. Para isso, vamos observar a ilustração da seção a seguir:

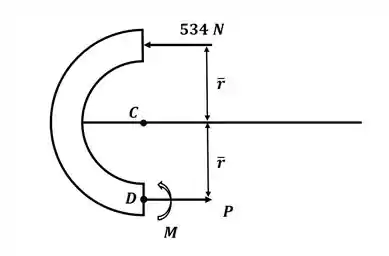
Agora nós vamos aplicar o somatório de forças na direção x para descobrir o valor da força P, então teremos:

+ → ∑ F x = 0

Substituindo os valores de acordo com o DCL acima, teremos:

P - 534 = 0 → P = 534   N

Agora para descobrir o valor do momento M, vamos aplicar o somatório de momento com relação ao ponto D, então teremos:

+ ↺ ∑ M D = 0

Substituindo os valores de acordo com o DCL, teremos:

2 r - 534 + M = 0 → M = - 2 0,02792 534 → M = - 29,818   N . m

Passo 3

Agora, para encontrar a tensão no ponto A pedida na letra (a), vamos utilizar a equação 4.71 vista nesse capítulo, lembrando que agora também temos a força de tração que deve ser somada a parcela de tensão gerada pelo momento. Então a equação 4.71 se torna:

σ A = M r A - R A e r A + P A

Substituindo os valores conhecidos, teremos:

σ A = - 29,818 0,0203 - 27,39.10 - 3 182,41.10 - 6 0,53.10 - 3 0,0203 + 534 182,41.10 - 6

σ A = 110,65   M P a

Passo 4

Agora para descobrir a tensão no ponto B pedida na letra (b), vamos repetir os cálculos do passo, só que agora com r B = r 2 = 35,54   m m . Então, teremos:

σ B = M r B - R A e r B + P A

Substituindo os valores conhecidos, chegamos em:

σ B = - 29,818 0,03554 - 27,39.10 - 3 182,41.10 - 6 0,53.10 - 3 0,03554 + 534 182,41.10 - 6

σ B = - 67,8   M P a

Resposta

a :   σ A = 110,65   M P a

b :   σ B = - 67,8   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Pede-se: (a) Mostrar que a tensão em um canto A de um membro retangular será nula, se a força vertical P for aplicada num ponto localizado sobre a linha x b / 6 + z h / 6 = 1 (b) Mostrar também que se
Em uma dada seção de um perfil laminado de aço S 200 × 34 , o efeito da gravidade é representado por um vetor-momento M 0 , Expressando por σ 0 a máxima tensão na viga quando θ = 0 , determinar o ângu
Uma viga de seção transversal assimétrica está submetida a um momento M z atuando em um plano vertical. Mostre que a tensão no ponto A de coordenadas y e z , é: σ A = - y I y - z I y z I y I z - I y z
Mostrar que: (a) Se uma força vertical P é aplicada no ponto A da seção mostrada, a equação do eixo neutro B D é x A k z 2 x + z A k x 2 z = - 1 Onde k z e k x , expressam os raios de giração da seção
Para que seja possível a entrada no interior de um tubo de seção quadrada de 6,35 m m de espessura, a porção B D de um dos lados do tubo foi removida. Sabendo-se que o carregamento no tubo é equivalen