Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 136b
Para o carregamento mostrado, sabendo-se que as vigas tem a mesma rigidez flexional, determinar a reação:
- Em D
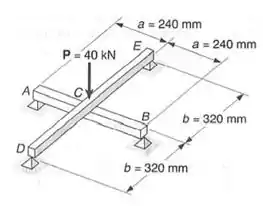
Passo 1
Então galerinha, nesse problema temos que tomar cuidado porque se trata de uma viga estaticamente indeterminada, e nesse caso vamos estar olhando primeiro a viga DCE, e aqui vamos usar um conceito novo.
Claro que não temos em vista um apoio de fato, mas podemos considerar que no ponto C temos uma espécie de apoio, que seria a própria viga inferior, assim, a nossa viga representada seria dada por:
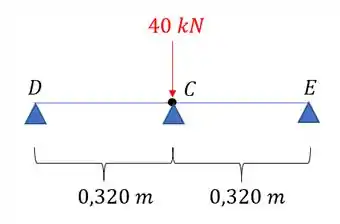
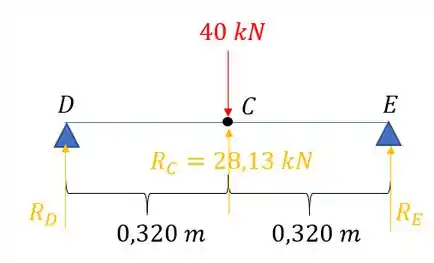
Vamos dividir a nossa viga em duas partes e com isso vamos romper o apoio em C e vamos trocar por uma reação.
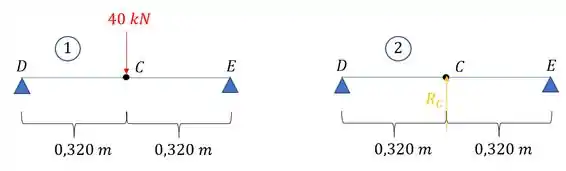
Passo 2
- Deformação no ponto C na viga 2
- Deformação no ponto C na viga 1
- Deformação no ponto C na viga 3
Sabemos que a tabela no fim do livro é dada por:
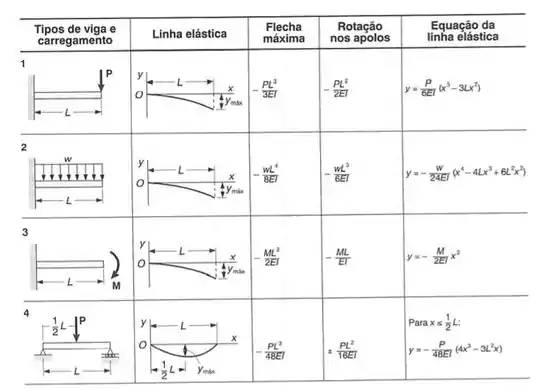
Por essa tabela vemos que a deformação no ponto C da viga para uma carga concentrada é dada por (e lembra como a carga é de baixo pra cima, vamos trocar o sinal da fórmula, assim, vamos ter que)
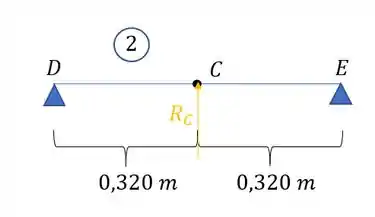
Pela tabela temos que a máxima deformação que ocorre no ponto C onde tem a deformação é dada por (lembrar que como a carga é de baixo pra cima, vai gerar uma deformação positiva):
Sabemos que a tabela no fim do livro é dada por:
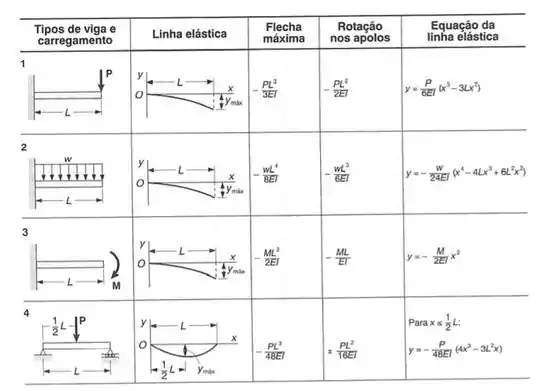
Por essa tabela vemos que a deformação no ponto C da viga para uma carga concentrada é dada por (e lembra como a carga é de baixo pra cima, vamos trocar o sinal da fórmula, assim, vamos ter que)
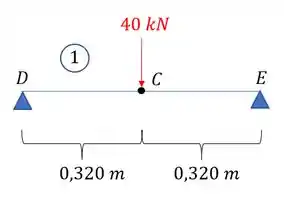
Pela tabela temos que a máxima deformação que ocorre no ponto C onde tem a deformação é dada por (lembrar que como a carga é de baixo pra cima, vai gerar uma deformação positiva):
Porém veja que determinamos o que ocorre com o ponto C quando olhamos ele pela barra de cima, porém, lembre-se que ele não é um apoio, logo, precisamos saber o que rola na nossa viga de baixo, para isso, é só transferir a nossa reação em C para a viga de baixo e determinar a deformação nesse ponto também, assim, teremos que:
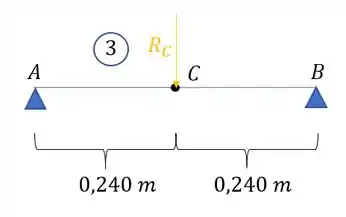
Usando a mesma fórmula, temos que:
Assim basta lembrar que a deformação do ponto C na barra de cima tem que ser igual a deformação no ponto C da barra de baixo, assim temos que:
Passo 3
Como nosso objetivo é determinar a reação no apoio em D, basta olharmos o que temos na nossa viga 1 e 2 juntas em uma só, assim, temos que:
