Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 69
Para o carregamento mostrado, (a) trace os diagramas de esforço cortante e momento fletor e (b) determine os valores absolutos máximos de momento e de cortante.
Passo 1
Fala aí galera, bora pra mais uma questão de estática. O primeiro passo é determinar as reações de apoio. Para determinar a reação em B, vamos fazer o somatório de momentos em A:
Passo 2
Para calcular as expressões para o esforço cortante e o momento fletor, vamos fazer cortes na nossa viga. Mas a força de 4 kN causa uma descontinuidade, então vamos ter que fazer 2 contas.
Primeiro vamos fazer um corte na viga, entre o ponto A e a força de 4kN, a uma posição de distância x do ponto A. Nesse ponto, tempos um esforço cortante V(x) e um momento fletor M(x), como na figura abaixo. E pra encontrar cada um deles fazemos o somatório de momentos no ponto de corte e o somatório de forças verticais. Essas equações vão valer pro intervalo em que x
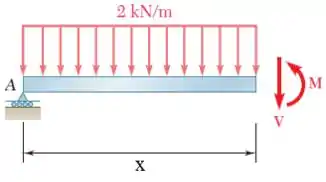
Agora, vamos fazer um corte entre a força de 4kN e o apoio em B, a uma distância x do ponto A. O diagrama de corpo livre fica como na figura abaixo. Fazendo o somatório de forças verticais, achamos o cortante. E o momento fletor, nós achamos fazendo o somatório de momentos no ponto de corte. Essas expressões vão valor pro intervalo em que x>3,2m.
Passo 3
Logo, o diagrama de esforço cortante fica:
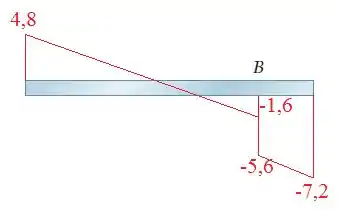
O diagrama de momento fletor fica:
Passo 4
Portanto, pelos diagramas podemos ver que os valores absolutos máximos de momento e cortante são: