Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 11
Cada membro da treliça é uniforme e possui peso . Remova a força externa e determine a força aproximada em cada membro em decorrência do peso da treliça. Indique se os membros estão sob tração ou compressão. Resolva o problema supondo que o peso de cada membro pode ser representado por uma força vertical, metade da qual é aplicada na extremidade de cada membro.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Vamos com muita calma nesta questão pois o início dela é bem confusa. Temos uma treliça simétrica sem aplicação de carga externa. Ela está suportando apenas o peso de cada membro.
Nosso objetivo aqui é determinar se os membros estão sob tração ou compressão e qual o valor desta força, como função de .
Mas como faremos isto? Nós precisamos começar analisando por algum nó que só tenha, no máximo, 2 incógnitas!
Bom, vamos começar obtendo as reações e no pino em e no rolete em . Pela simetria do problema, podemos afirmar que .
Além disto, como a treliça possui 7 membros, o peso total é na direção vertical. Logo, as reações e serão:
E agora já temos um ponto de partida, o ponto !
OBS: Poderia ser o ponto , pois temos , já que não existe nenhuma força horizontal.
Passo 2
Agora vamos utilizar o método dos nós para analisar cada um deles.
Mas, antes disto, devemos sempre lembrar de colocar a componente de metade do peso em cada nó. Isto é, por exemplo, se em um determinado nó chegam 4 membros, então, deverá haver uma força vertical para baixo de intensidade .
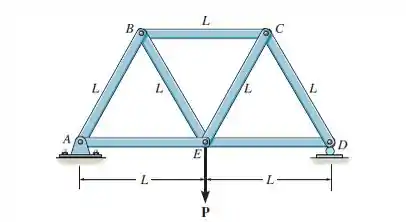
Para o caso do nó , como chegam membros, teremos uma força de intensidade para baixo! Esboçando o diagrama de equilíbrio, temos:
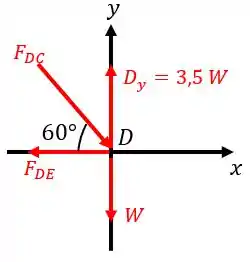
Utilizando as relações de equilíbrio, temos:
Resolvendo o sistema acima obtemos:
OBS: Lembrem-se, quando a direção da força é no sentido de entrar no nó (seta no nó), a força é de compressão. Caso contrário, é de tração.
Passo 3
Agora, vamos fazer a mesma análise de nós, só que para o nó .
Como chegam 3 membros para este nó, a força vertical para baixo será igual a . Então, esboçando o diagrama de equilíbrio, temos:
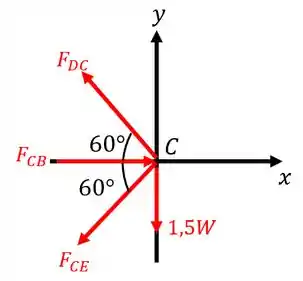
Percebam que a força mudou de sentido em relação ao caso do nó por questão de ação e reação. Entretanto, continua sendo uma força de compressão na mesma direção!
Continuando, basta agora resolvermos as equações de equilíbrio. Logo,
Resolvendo o sistema acima obtemos:
Passo 4
Para finalizarmos a questão, temos que determinar a força sobre os outros membros.
Entretanto, como a treliça é simétrica, o carregamento nos outros membros simétricos serão o mesmo que obtemos nos passos anteriores. Portanto,
E assim finalizamos a questão!