Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 65

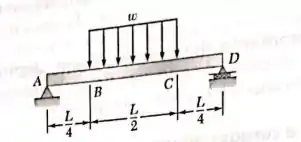
Utilizando o método da seção 7.6, resolva o problema 7.31.

Passo 1

Fala aí galera, vamos para mais um problema de estática. Para traçar os diagramas pelo método pedido, vamos encontrar a função que rege o cortante e o momento. Vamos caminhar com uma distância x arbitrária da esquerda para a direita (de A até C).

Primeiro, vamos fazer de 0 até L 4 :

C = w L 4

M = w L 4   × x = w L x 4

Agora, vamos fazer de L 4 até 3 L 4 :

C = w L x 4 - w x ' - L 4

M = w L 4 x ' - w L 2 ( x ' - L 4 2 )

De 3 L 4   até L (invertemos o sentido para facilitar):

C = - w L 4

M = w L 4   × x ' ' = w L x ' ' 4

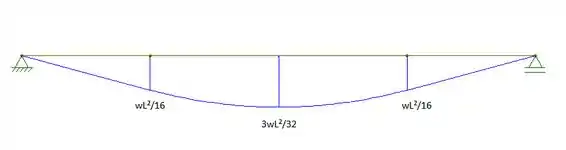
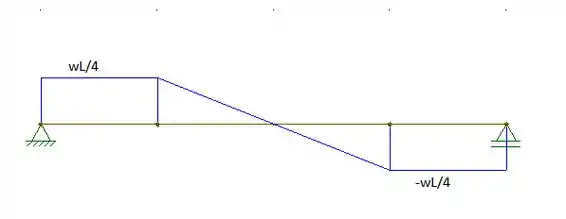
Logo, os diagramas serão:

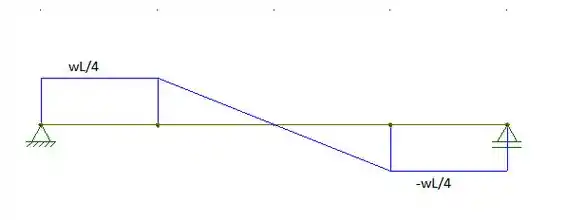
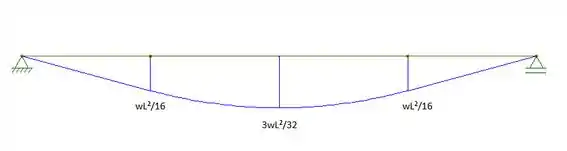
Passo 2

Como podemos ver nos diagramas, os valores máximos absolutos de momento e cortante são:

M = 3 w L 2 32

V = w L 4

Resposta

  2. M = 3 w L 2 32 ;   V = w L 4
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma tubulação de óleo é sustentada em intervalos de 1,8m , por ganchos verticais presos ao cabo mostrado na figura. Em razão do peso combinado do tudo e seu conteúdo, a tração em cada gancho é de 1800
29. Para a viga e o carregamento mostrados nas figuras, (a) trace os diagramas de esforço cortante e de momento fletor, (b) determine os valores absolutos máximos do esforço cortante e do momento flet
30. Para a viga e o carregamento mostrados nas figuras, (a) trace os diagramas de esforço cortante e de momento fletor, (b) determine os valores absolutos máximos do esforço cortante e do momento flet
31. Para a viga e o carregamento mostrados nas figuras, (a) trace os diagramas de esforço cortante e de momento fletor, (b) determine os valores absolutos máximos do esforço cortante e do momento flet
32. Para a viga e o carregamento mostrados nas figuras, (a) trace os diagramas de esforço cortante e de momento fletor, (b) determine os valores absolutos máximos do esforço cortante e do momento flet