Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 70
A chave elétrica fecha quando as hastes de ligação e se aquecem, o que provoca a translação e a rotação do braço rígido até fechar o contato em . A posição original de é vertical e a temperatura é . Se for feita de bronze e , de alumínio , determine o espaço exigido entre os contatos para a chave fechar quando a temperatura alcançar .
Passo 1
Um braço rígido é mantido vertical por duas hastes, e , quando a temperatura é . As hastes são aquecidas até .
Características da haste :
- Bronze : . (Tabelado)
- Comprimento inicial: .
- Alumínio : . (Tabelado)
- Comprimento inicial: .
Características da haste :
O aquecimento das hastes e causará expansão térmica, aumentando o comprimento delas: e
No ponto , no topo do braço, temos um contato que fecha uma chave elétrica se tocar em .
A variação de temperatura vai fazer o ponto se mover um comprimento .
Entre e há um vão de comprimento , desconhecido! Queremos saber qual tamanho esse vão deve ser para que no aquecimento o ponto toque em . Ou seja, queremos:
Precisamos descobrir !
Passo 2
Com o aumento de temperatura, as hastes vão expandir. Mas elas são feitas de materiais diferentes, então vão ter tamanhos diferentes no final!
Veja que , então a haste superior vai aumentar mais que a inferior! O braço rígido vai ficar inclinado para a direita.
Vamos ver como os deslocamentos se relacionam.
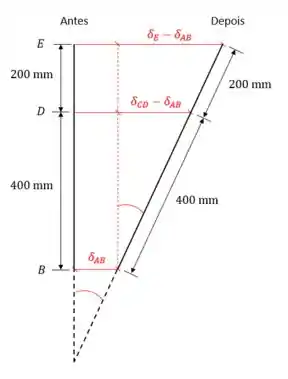
Usando a tangente do ângulo demarcado na figura:
Show! Pra achar o deslocamento de vamos precisar calcular o quanto as hastes expandiram por efeito da mudança de temperatura.
Passo 3
Aplicamos a fórmula da expansão térmica para cada haste:
Passo 4
Use os valores de e na relação com :
Então o vão precisa ser
Resposta
Espaço entre os contatos: .