Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 86
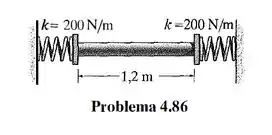
A haste é feita de aço e tem diâmetro de . Se as molas forem comprimidas quando a temperatura da haste é , determine a força na haste quando sua temperatura for .
Passo 1
Fala, vamos entender a situação.
Uma haste de aço é mantida entre duas molas. Essas molas tem uma deformação incial. A haste sofre uma mudança de temperatura Essa mudança aumenta a haste, comprimindo ainda mais as molas. Ele quer a força final nas molas, resultado dessas duas deformações.
Características da haste:
- Aço: , . (tabelado)
- Área transversal: .
- Comprimento inicial: .
- Temperatura inicial: . Temperatura final: .
- Rigidez das molas nas extremidades: (considere essa unidade!)
As molas que dão suporte à haste já estão pressionadas um comprimento , o que causa uma certa compressão na haste como resposta.
Quando ocorre a variação de temperatura, , ocorre dilatação térmica na haste. As molas vão resistir esse avanço, aumentando a força de compressão na haste para .
Queremos descobrir essa força !
Passo 2
Dois efeitos ocorrem na haste:
- O aumento de temperatura vai causar uma expansão da haste: .
- A reação das molas vai comprimir mais o tubo, reduzindo: .
Antes do aquecimento, cada mola já estava comprimida . Depois do aquecimento, cada mola irá sofrer um deslocamento adicional da extremidade dela (deflexão).
A força total gerada por uma mola é
Enfatizando: o nessa equação é o quanto cada mola foi comprimida depois que a haste foi aquecida e é a deformação inicial.
Agora, repare no seguinte. Quando a haste se expande, ele aumenta o comprimento nas duas extremidades ao mesmo tempo. Como estamos com as mesmas condições dos dois lados da haste (isso não acontece sempre, cuidado!), em cada lado a haste aumenta .
Juntando tudo isso numa equação de compatibilidade: o tubo aumenta , reduz , resultando em um aumento de ( para cada extremidade).
Repara que a gente não colocou o ali porque essa equação se refere ao que acontece com a mudança de temperatura.
E por causa de , temos como relacionar com a força que a questão pede!
Passo 3
Show! Temos fórmulas pra esses deslocamentos!
Expansão térmica:
Relação carga-deslocamento:
Vamos substituir tudo que sabemos pra dar uma facilitada na equação:
Isole :
Passo 4
Agora é só substituir os valores:
Resposta
Força na haste: .