Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 75
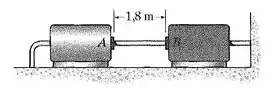
Um tubo de vapor com de comprimento é feito de aço com e está ligado diretamente a duas turbinas e , como mostra a figura. O diâmetro externo do tubo é e a espessura da parede é . A ligação foi feita a . Considerando que a rigidez dos pontos de acoplamento das turbinas é , determine a força que o tubo exerce sobre elas quando o vapor e, portanto, o tubo, atingem uma temperatura de .
Passo 1
Fala, querido!
Um tubo mantido entre duas turbinas é aquecido. Os acoplamentos nas turbinas são elásticos, com rigidez .
Ele quer a força nesses acoplamentos. Vamos pensar que eles são como molas. A ideia é que nosso tubo vai esticar por causa do aumento de temperatura, causando uma deformação nessas molas. Essa deformação gera então uma força nessas molas. Precisamos descobrir o valor delas.
Características do tubo:
- Aço: , . (tabelado)
- Diâmetro externo: . Espessura:
- Comprimento inicial: .
- Temperatura inicial: . Temperatura final: .
A variação de temperatura no tubo, , irá causar uma expansão térmica. As turbinas vão resistir esse avanço, comprimindo o tubo com uma força .
Queremos descobrir essa força !
Passo 2
Dois efeitos ocorrem no tubo:
- O aumento de temperatura vai causar uma expansão do tubo: .
- A reação dos acoplamentos vai comprimir o tubo, reduzindo: .
Os acoplamentos são elásticos, então a força que comprime o tubo vai seguir a relação linear
O nessa equação é o quanto cada acoplamento elástico fica comprimido! Você pode imaginar esses acoplamentos exatamente como molas, uma em cada ponta do tubo.
Fique atento que o tal é o movimento (deflexão) em cada mola!
Quando o tubo se expande, ele aumenta o comprimento nas duas extremidades ao mesmo tempo. Como estamos com as mesmas condições dos dois lados do tubo (isso não acontece sempre, cuidado!), em cada lado o tubo aumenta .
Juntando tudo isso numa equação de compatibilidade: o tubo aumenta por causa do aumento de temperatura, reduz por causa das reações das turbinas que causam compressão, resultando em um aumento de (um para cada extremidade do tubo).
E por causa de , temos como relacionar com a força que a questão pede!
Passo 3
Show! Temos fórmulas pra esses deslocamentos!
Expansão térmica:
Relação carga-deslocamento:
Vamos substituir tudo que sabemos pra dar uma facilitada na equação:
Repara que é a força gerada nos acomplamentos. E essa mesma força é a que tende a comprimir nosso tubo. Porque as molas nesses acomplamentos tendem a esticar, causando essa essa força no tubo.
Isole :
Passo 4
Precisamos da área do tubo. Ele é um cilindro vazado. O diâmetro externo é . O diâmetro interno vai ser o externo menos duas vezes a espessura ! Então .
Área do tubo:
O que a questão pediu acaba aqui! Porém, é bom conferir mais uma coisa.
Passo 5
A questão nos deu o valor da tensão de escoamento: . Tudo isso que fizemos foi assumindo que a expansão térmica ocorre no regime elástico do material! Vamos ver se essa hipótese é verdade.
Tensão axial provocada pela compressão no tubo:
Show, . Então está tudo certo! Estamos no regime elástico e nosso resulto é válido.
Resposta
Força no tubo: .