Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 111
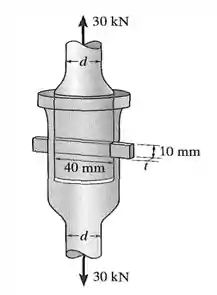
A chaveta é usada para manter as duas hastes juntas. Determine a menor espessura da chaveta e o menor diâmetro das hastes. Todas as partes são feitas de aço com tensão de ruptura por tração e tensão de ruptura por cisalhamento . Use um fator de segurança em tração e em cisalhamento.
Passo 1
Desejamos encontrar o valor mínimo da espessura da chaveta e o menor diâmetro das hastes e, para isso, vamos utilizar as fórmulas das tensões de cisalhamento e normal que são dadas pelas seguintes fórmulas
Onde
Dessa forma, vamos obter
Passo 2
Analisando a fórmula da tensão normal vamos ter
Onde
Dessa forma, vamos obter
Por fim, aplicando a fórmula da tensão de cisalhamento vamos obter
Resposta
Exercícios de Livros Relacionados
Para a viga com o carregamento mostrado, dimensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 860k P a .
Para a viga com o carregamento mostrado, domensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 825k P a .
Para a viga com o carregamento mostrado, domensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 825k P a .
Para a viga com o carregamento mostrado, domensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 825k P a .
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado e determinar o máximo valor absoluto a) força cortante b) momento fletor.