Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 104
A barra está acoplada ao suporte por um pino de diâmetro . Se a tensão de tração admissível para a barra for e a tensão de apoio admissível entre o pino e a barra for , determine as dimensões e tais que a área bruta da área da seção transversal seja e a carga seja máxima. Qual é essa carga máxima? Considere que o orifício na barra tem o mesmo diâmetro do pino.
Passo 1
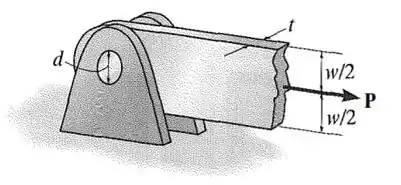
Falaaa! O que está acontecendo ali é que a gente tem a força que vai causar tração na barra, e, essa barra vai causar um esforço normal na seção do pino que está em contato com a barra e perpendicular a .
Desejamos encontrar os valores das dimensões e de tal forma que .
Além disso queremos que esse fato implique em uma carga tendo seu valor máximo e, para isso, devemos relacionar esses valores que desejamos encontrar com as equações que regem as tensões admissíveis dadas no problema.
A fórmula para tensão máxima média é:
Aí vamos reunir nossos dados:
Bora lá, resolver!
Passo 2
Podemos tentar montar um sistema com os dados e as equações que temos, aí talvez consigamos encontrar o que a questão nos pede. Dessa forma, teremos
Para achar as outras equações, vamos usar a fórmula da tensão máxima média. Para a tensão normal na seção da barra temos:
Esse vai ser a menor seção transversal da barra (para a tensão ser máxima). Ela ocorre onde temos o pino. Então:
E para o pino, a seção dele que é normal a é . Então temos:
Resolvendo o sistema composto por essas 3 equações vamos encontrar