Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 108

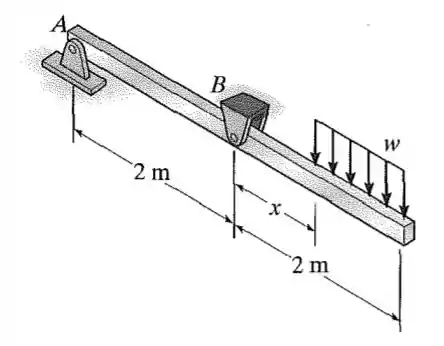
A barra é mantida em equilíbrio por pinos em A   e   B . Observe que o apoio em A tem uma única orelha, o que envolve cisalhamento simples no pino, e o apoio   B tem orelha dupla, o que envolve cisalhamento duplo. A tensão de cisalhamento admissível para ambos os pinos é τ a d m   =   125   M P a . Se x   =   1   m e w   =   12   k N / m , determine o menor diâmetro exigido para os pinos A   e   B . Despreze qualquer força axial na barra.

Passo 1

Desejamos encontrar o valor dos diâmetros dos pinos A   e   B . Primeiramente, vamos calcular os momentos em A   e   B , tomando o sentido anti-horário como positivo, conseguimos encontrar as forças necessárias usarmos nas equações de tensão e, assim, podemos relacionar com o diâmetro

∑ M A = 0 → B y ⋅ 2 m - w ⋅ 2 - x ⋅ 2 + x + 2 - x 2 = 0   → B y = 21   k N

∑ M b = 0 → A y ⋅ 2 m - w ⋅ 2 - x ⋅ x + 2 - x 2 = 0 → A y = 9   k N  

Passo 2

Agora, basta substituir nas equações de tensão de cisalhamento e vamos obter

A = A y τ a d m → π 4 ⋅ d A = A y τ a d m

d A = 4 π ⋅ A y τ a d m ≈ 9,57 m m

Para o pino B vamos ter a mesma coisa com a diferença que a força será dividida por 2 devido ao cisalhamento duplo

A = ( 0,5 ) B y τ a d m → π 4 ⋅ d A = B y τ a d m

d A = 2 π ⋅ B y τ a d m ≈ 10,34   m m

Resposta

d a = 9,57   m m   e   d b = 10,34   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar a localiz
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar a localiz
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar a localiz
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar a localiz
Para a viga com o carregamento mostrado, domensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 825k P a .