Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 8.Problemas - Ex. 104
Um cilindro de , que está preso a uma pequena polia , é colocado na corda conforme a figura. Determine o maior ângulo de modo que a corda não deslize pelo pino em . O cilindro em tem uma massa de e o coeficiente de atrito estático entre o pino e a corda é
Passo 1
A liustração que ele comenta no enunciado é a seguinte:
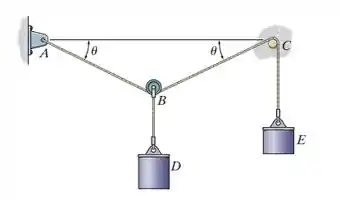
Passo 2
Como nosso sistema está em equilíbrio, a força resultante é nula. Logo, olhando a para polia :
Substituindo os valores:
Passo 3
Agora que já sabemos a tração da corda, basta usar aquela formulinha da teoria, se liga só:
Onde se opõe ao movimento e atua na direção do movimento.No nosso caso, e . Além disso, nosso será
Assim,
Portanto,
Resolvendo por tentativa e erro, temos:
Resposta
Exercícios de Livros Relacionados
A viga lisa está sendo içada por meio de uma corda envolvendo a viga e passando por um anel em A , conforme mostrado. Se a extremidade da corda está sujeita a uma tração T e o coeficiente de atrito es
Uma correia em “ V ” é usada para conectar o eixo A do motor à roda B . Se a correia pode sustentar uma tração máxima de 1200N , determine a maior massa do cilindro C que pode ser levantada e o torque
O bloco A tem massa de 50k g e repousa sobre uma superfície para a qual μ s = 0,25 . Se o coeficiente de atrito estático entre a corda e o pino fixo em C é μ s ' = 0,3 , determine a maior massa do cil
O bloco A se apoia sobre a superfície para a qual μ s = 0,25 . Se a massa do cilindro suspenso D é 4k g , determine a menor massa do bloco A para que ele não deslize ou tombe. O coeficiente de atrito
Os blocos A e B têm massas de 20 kg e 10 kg, respectivamente. Usando os coeficientes de atrito estático indicados, determine a maior massa do bloco D sem causar movimento.