Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 112

Um cilindro de 50 mm de diâmetro de 30 in. de diâmetro é feito de latão para qual o diâmetro tensão-deformação está apontado. Sabendo que o ângulo de giro é de 5° em um comprimento de 725 mm, determine por método aproximado a intensidade T do torque aplicado no eixo.

Passo 1

E ai galera tudo certo? O enunciado pede que a gente determine determine por método aproximado a intensidade T do torque aplicado no eixo.. Então partiu?

φ = 5 ° = 87,266   x   10 - 3 r a d c = 1 2 d = 0,25   m       L = 0,725   m   γ m a x = c φ L = 0,025   x   ( 87,266   x   10 - 3 ) 0,725 = 0,00301

Onde:

z = γ γ m a x = ρ c T = 2 π ∫ 0 c p ² τ d ρ = 2 π c 2 3 ∫ 0 1 z ² τ d z = 2 π c 2 3 I onde o integral I é dado por I = ∫ 1 / 3 1 z ² τ d z

Avaliar I usando um método de integração numérica. Se a rega de Simpson for usada, a fórmula de integração é:

I = ∆   z 3 ∑ w z ² τ

Onde o W é um fator de ponderação. Usando ∆   z = 0,25 , obtemos os valores fornecidos na tabela abaixo.

Passo 2

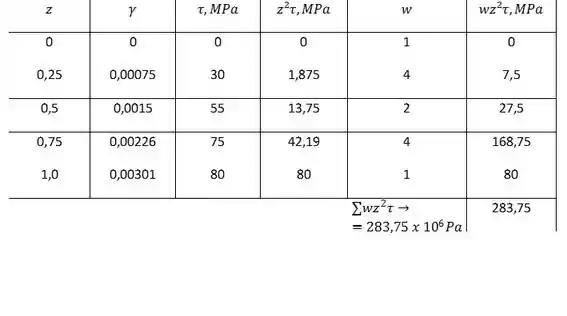
Calculando a inércia temos:

I = 0,25   x   ( 283,75   x   10 6 ) 3 = 23,65   x   10 6 P a

T = 2 π c ³ I = 2 π   x   0,025 3   x   23,65   x   10 6 = 2,32   x   10 3 N . m  

Resposta

T = 2,32 k N   . m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo cheio AB tem um diâmetro d s = 1.75i n e é feita de aço com G = 11.2 × 10 6 p s i e τ a l l = 12K s i , enquanto a luva CD é feita de latão com G = 5.6 × 10 6 p s i e τ a l l = 7K s i . Determi
O navio em A está começando a perfurar um poço de petróleo no fundo do oceano a uma profundidade de 1524 m. Sabendo que o topo da broca de aço G = 77,2G P a de 203 mm de diâmetro dá duas voltas comple
O eixo cheio AB tem diâmetro d s = 1.5i n , e é feito de aço com G = 11,2X 10 6 psi e τ a l l = 7 psi, enquanto a luva CD é feita de latão com G=5,6 x 10 6 psi e τ a l l = 7 ksi. Determine o maior âng
Três eixos se seção transversal cheia são conectados pelas engrenagens A e B mostradas. Sabendo que G = 77,2 GPa, determine o ângulo de torção entre (a) A e B (b) A e C.
(a) Para o eixo de alumínio mostrado G = 27G P a , determine o torque T 0 que provoca um ângulo de torção de 2° e (b) o ângulo de torção provocado pelo mesmo torque T 0 em um eixo cilíndrico cheio de