Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 36

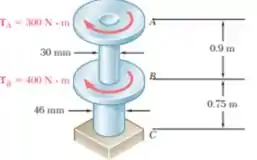
Três eixos se seção transversal cheia são conectados pelas engrenagens A e B mostradas. Sabendo que G = 77,2 GPa, determine o ângulo de torção entre

(a) A e B

(b) A e C.

Passo 1

Bora lá, vamos ver o ângulo de torção entre A e B.

T A B = 300   N / m , L A B = 0.9   m

C A B = 1 2 d = 0.015   m

J A B = π 2 c 4 = π 2 0.015 4 = 79.522 × 10 - 9 m 4

ϕ A B = T A B L A B G J = 300 0.9 77.2 × 10 9 79.522 × 10 - 9 = 43.980 × 10 - 3 r a d

ϕ A B = 2.52 °

Passo 2

Podemos prosseguir para o eixo BC!

  T BC = 300 + 400 = 700   N/m , L CD =0.75 m ,

C BC = 1 2 d=0.023 m ,

  J BC = π 2 c 4 = π 2 0.023 4 =439.57× 10 -9 m 4

  ϕ BC = 700 0.75 77.2× 10 9 439.57× 10 -9 = 15.4708 -3 rad

ϕ BC = 0.89 °

ϕ AC = ϕ BC + ϕ BC =2.52°+0.89 ° = 3.41 °

Resposta

  1. A B = 2.52 °
  2. AC = 3.41 °
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o Prob. 3.47, considerando que AB é feito de aço ( G = 77G P a ) , ao invés de alumínio
A barra cilíndrica maciça AB e o tubo CD são ambos unidos por um pequeno cilindro E. A barra cilíndrica AB é de aço, com G a = 77G P a e τ a d m a = 84M P a ; enquanto que o tubo CD é de latão, com G
Sabendo-se que um torque T de 2,3k N m é aplicado ao cilindro E do Prob. 3.49, determinar (a) a máxima tensão de cisalhamento na barra cilíndrica AB; (b) a máxima tensão de cisalhamento no tubo CD
Uma placa anelar de espessura t e módulo de elasticidade transversal G é usada para conectar o Eixo AB de raio r 1 ao tubo CD de raio interno r 2 . Sabendo-se que o torque T é aplicado à extremidade A
Uma placa anelar de espessura t e módulo de elasticidade transversal G é usada para conectar o Eixo AB de raio r 1 ao tubo CD de raio interno r 2 . Sabendo-se que o torque T é aplicado à extremidade A