Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 26

O cilindro hidráulico CF, que controla parcialmente a posição da haste DE, foi travado na posição mostrada. O elemento BD tem 15 mm de espessura e está conectado em C à haste vertical por um parafuso de 9 mm de diâmetro. Sabendo que P= 2 kN e Ø= 75°, determine (a) a tensão de cisalhamento média no parafuso, (b) a tensão de contato em C no elemento BD.

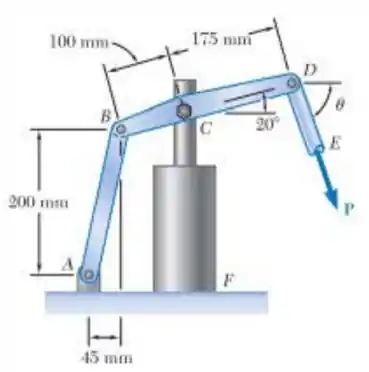
Passo 1

  1. E aí gurizada tudo belezinha??? Antes de mais nada vamos desenhar o diagrama de corpo livre para facilitar os cálculos?

+ ↺ ∑ M c = F × d = 0

40 41 F A B   ( 100 cos ⁡ 20 ) - 9 4 F A B   ( 100 sen ⁡ 20 ) = 0

- 2 K N cos ⁡ 75   ( 175   sen ⁡ 20 ) - 2   K N   ( 1 ⁡ 75 ) ( s e n   75 + 20 ) = 0

100 41 F A B   ( 40 cos ⁡ 20 - 9   s e n   20 ) = 2 k N × 175 ( sen ⁡ 75 + 20 )

F A B = 4,14   K N

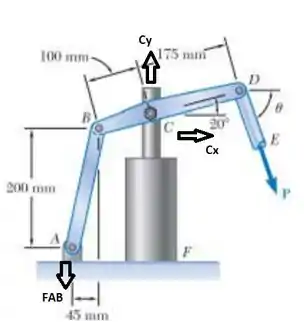
Agora gurizada devemos realizar o somatório de forças em x :D

+ → ∑ F x = 0

C x - 9 41 4,14   x   10 3 + 2   x 10 3 cos ⁡ 75 = 0

C x = 0,4     x 10 3   N

Agora devemos realizar o somatório de forças em y :D

+ → ∑ F y = 0

C y - 40 41 4,14   x   10 3 + 2   x 10 3 sen ⁡ 75 = 0

C y = 5,98     x 10 3   N

Passo 2

  1. Para calcularmos a tensão de cisalhamento média no parafuso

    2. τ = C A  

    τ = 5,98   × 10 3 π × 0,0045 2  

    τ = 94,1     M P a

    Passo 2

  2. Para calcularmos a tensão de contato em C no elemento BD

τ = C t d

σ = 5,98   × 10 3 / ( 0,015 × 0,009 )  

σ = 44,3   M P a

Resposta

  1. 94,1     M P a
  2. 44,3   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O parafuso longo passa pela chapa de 30 m m de espessura.Se a força na haste do parafuso for 8 k N , determine a tensão normal média na haste, a tensao de cisalhamento média ao longo da área cilíndric
O punção circular B exerce uma força de 2k N na parte superior da chapa A . Determine a tensão de cisalhamento média na chapa provocada por essa carga.
O acoplamento de gancho e haste está sujeito a uma força de tração de 5k N . Determine a tensão normal média em cada haste e a tensão de cisalhamento média no pino A entre os elementos.
Duas pranchas de madeira, cada uma com 12 mm de espessura e 225 mm de largura são unidas pela junta de encaixe mostrada na figura. Sabendo que a madeira utilizada rompe por cisalhamento ao longo das f
A força axial na coluna que suporta a viga de madeira mostrada é P= 75KN. Determine o menor comprimento L admissível para chapa de contato para que a tensão de contato na madeira não exceda 3 MPa.