Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 112
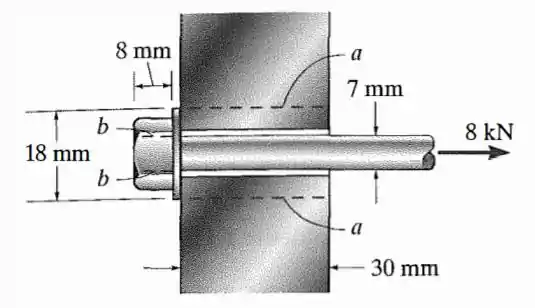
O parafuso longo passa pela chapa de de espessura.Se a força na haste do parafuso for , determine a tensão normal média na haste, a tensao de cisalhamento média ao longo da área cilíndrica da chapa definida pelas linhas de corte e a tensão de cisalhamento média na cabeça do parafuso ao longo da área cilíndrica definida pelas tinhas de corte
Passo 1
Oláaaaaa, querido! Tá bem?
Então, a gente quer encontrar o valor da tensão normal média na haste e, além disso, encontrar as tensões de cisalhamento média para as seções e .
Vamos começar pela tensão normal, tá bem? Ela tem essa fórmulinha:
Onde é a força axial de e é a área da seção transversal da haste circular:
Onde . Logo podemos calcular a tensão assim:
Passo 2
Agora vamos olhar para o cisalhamento na seção .
Lembrando que a tensão de cisalhamento é dada por
Onde é uma área cilíndrica (área da lateral do cilindro) que o enunciado diz que sofre cisalhamento. Então
Mas que força causa cisalhamento nela? Cara, parafuso é puxado pela força . E aí a arruela tenta segurar ele. E para isso ela aplica um esforça de na chapa. Esse forço é paralelo a , então ele causa nosso cisalhamento
Aí tensão fica
Passo 3
Agora para a seção , temos que ela é cilíndrica também. Aí a área dela também é a área lateral do cilindro.
Temos que a força paralela a essa área é novamente . Então nossa tensão fica: