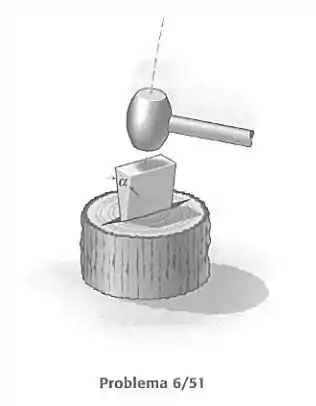
Se o coeficiente de atrito entre a cunha de aço e as fibras úmidas de um tronco recentemente cortado vale 0,20, deternube i ângulo máximo que a cunha pode ter para não pular fora da madeira após ter sido atingida pela marreta.
Passo 1
Após a marreta atingir a cunha, ela afunda na fenda do tronco, e então sofre forças de contato do tronco pelos dois lados, como mostra a figura:
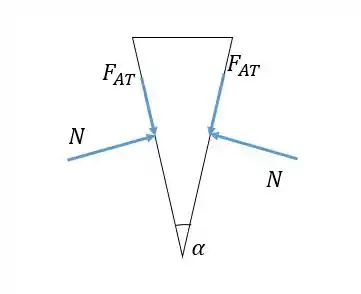
Como podemos ver atuam na cunha as componentes normais e o atrito. Note que o atrito deve ser para baixo, pois se não sempre teríamos resultante para cima (já que a normal já aponta para cima). O problema quer o ângulo máximo de abertura da cunha para o qual ela não irá subir. Isso corresponde a dizer que a força resultante do atrito com a normal não é para cima! No caso limite, onde teremos o ângulo máximo, a força resultante é horizontal, e qualquer aumento de fará com que exista uma componente da resultante apontando para cima.
Passo 2
Vamos então calcular o ângulo para o nosso caso limite. Posicionamos a resultante na horizontal:
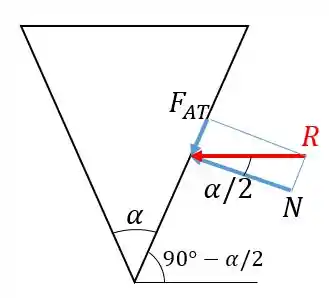
Pela figura, vemos que:
Mas o problema diz que o coeficiente de atrito é 0,20. Então:
Com isso: