Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 130
Calcule o momento da força de em relação ao eixo -.
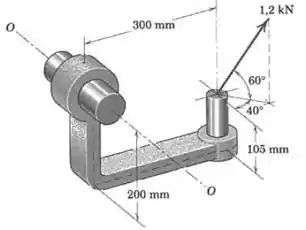
Passo 1
Uma boa forma de resolver esse problema é calcular o momento de cada componente da força em relação ao eixo .
Lembrando que a definição de momento em três dimensões é um pouco mais rigorosa:
Onde é o vetor unitário na direção do eixo -, e é o vetor posição que vai de qualquer ponto do eixo até o ponto onde a força é aplicada.
Vamos aplicar essa fórmula para calcualr o momento de cada uma das componentes da força.
Passo 2
Começamos com a componente , que tem um vetor posição . Tente aplicar a regra da mão direita do produto vetorial para entender o desenho:
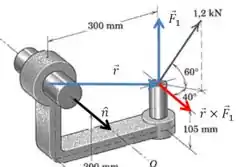
Lembre que só o que importa para o produto vetorial é a componente de que é perpendicular à força .
Como o momento (seta vermelha) é paralelo ao eixo - (ou seja, ao vetor ):
E então:
Passo 3
Agora vamos seguir a mesma lógica para as outras componentes:
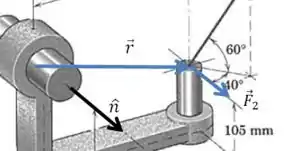
Para essa componente da força nem sequer precisamos calcular o momento. Quando a força é paralelo ao eixo (ou seja, paralela ao vetor ) o momento em relação ao eixo é sempre nulo:
Isso acontece porque o termo entre parênteses sempre será perpendicular a , e quando é paraleleo a , o termo também será perpendicular a . E o produto escalar de dois vetores perpendiculares é zero!
Passo 4
Agora vamos para a última componente:
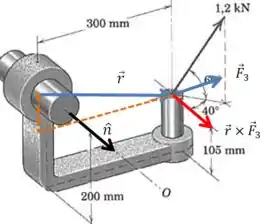
E temos um caso muito parecido com o do passo , mas agora a componente perpendicular do vetor é a diferença de altura entre os pontos:
Passo 5
E agora é só somar os momentos que calculamos:
E então:
Resposta
O momento da força em relação ao eixo é .