Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 53
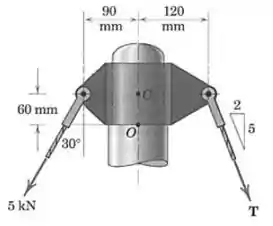
A presilha no topo de um mastro suporta as duas forças mostradas. Determine o módulo de que não causará momento (momento nulo) no ponto .
Passo 1
Vamos considerar o momento de cada uma das forças em relação ao ponto . Começando pela força de , que chamaremos de .
Podemos decompor a força em duas componentes, e então calcular o momento de cada um deles. Na direção horizontal temos:
E essa força é aplicada na altura do ponto , então:
Agora podemos usar a mesma lógica para a componente vertical fa força:
E então o momento total da força é:
Passo 2
Agora vamos fazer o mesmo para a força . Dessa vez um sinal negativo deve aparecer nos momentos, já que as forças favorecem a rotação no sentido contrário ao da força .
Podemos encontrar o ângulo que forma com a vertical usando o triângulo retângulo que foi dado na figura. Lembrando que, pelo teorema de pitágoras:
Então:
Agora é só substituir:
Passo 3
Agora queremos que esses dois momentos estejam em equilíbrio:
Resposta
O módulo da tração deve ser .