Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 64
O coeficiente de atrito estático para ambas as superfícies da cunha é de 0,40 e o entre o bloco de concreto de 27 kg e a inclinação de 20 ∘ é de 0,70. Determine o valor mínimo da força P necessária para começar a mover o bloco subindo a inclinação. Despreze o peso da cunha.
Passo 1
Primeiro, vamos desenhar o diagrama do corpo livre
Peso do bloco é
Uma vez que ângulo de fricção são
Observe que, para que o bloco deslize, a cunha também precisa deslizar, portanto, ambas as forças de atrito em A e B são forças de atrito máximas
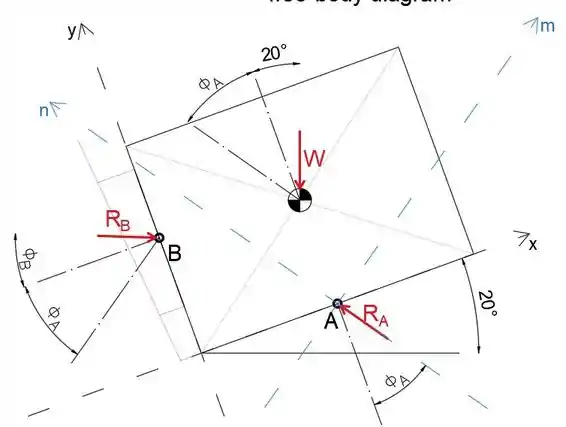
Ao igualar a soma das forças na direção-m a zero, podemos determinar a força de reação em B
Passo 2
A seguir, desenharemos o diagrama de corpo livre da cunha
Observe que o deslizamento ocorre simultaneamente em B e C
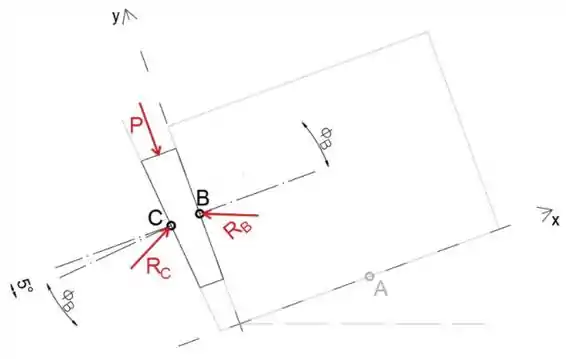
Equacionando a soma das forças na direção x a zero, podemos determinar a força RC
Finalmente, ao igualar a soma das forças na direção y a zero, podemos determinar a força P necessária para mover a roda