Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 208
As seções triangulares e retangulares estão sendo consideradas para o projeto de uma pequena barragem de concreto de água doce. Do ponto de vista da resistência ao capotamento em torno de C, qual seção exigirá menos concreto e quanto menos por metro de comprimento da barragem? O concreto pesa 150 lb / ft ³.
Passo 1
Em primeiro lugar, precisamos calcular a pressão que atua na parede a partir da água. Observe que a pressão é igual nas paredes A e B, pois a profundidade da água é a mesma.
Observe também que a água está sempre agindo normal à superfície, e a expressão para pressão na profundidade h é:
Uma vez que o peso específico da água doce é: γw = 62,4 lb / ft³, e a profundidade da água é h = 24’', a pressão na parte inferior da parede é:
Observe que este é um problema tridimensional, que podemos resolver como bidimensional, colocando a pressão que atua na parede para atuar de uma vez. Vamos considerar o comprimento de 1 pé, então a pressão da água atuando no comprimento de 1 pé da parede é:
Passo 2
bloco A
Agora, vamos isolar e desenhar o diagrama de corpo livre do bloco A. Observe que consideraremos o comprimento de 1 pé do bloco, mas calculamos a pressão da água para o comprimento de 1 pé.
O peso do bloco é igual ao produto de seu volume e peso específico. e atua em seu centróide.
Para comprimento de 1 pé, o volume do bloco é:
Como o peso específico do bloco é γe = 150 lb / ft ³, o peso W pode ser calculado
Como a pressão que atua no bloco é uma carga distribuída, podemos substituí-la por seu P resultante atuando no centróide do triângulo.
Equacionando a soma dos momentos sobre o ponto C a zero, determinaremos o peso necessário para resistir ao tombamento sobre C.
Substitua e pelos valores calculados no passo acima.
Expressaremos a como:
Podemos calcular a quantidade de concreto necessária para resistir ao tombamento, colocando o valor de a na expressão (1)
Passo 3
bloco B
Agora, vamos isolar e desenhar o diagrama de corpo livre do bloco B. Observe que consideraremos o comprimento de 1 pé do bloco, uma vez que calculamos a pressão da água para o comprimento de 1 pé.
O peso do bloco é igual ao produto de seu volume e peso específico. e atua em seu centróide.
For 1 -ft comprimento, volume do bloco é:
Uma vez que o peso específico do bloco é , o peso pode ser calculado.
Como a pressão que atua no bloco é uma carga distribuída, podemos substituí-la por seu P resultante atuando no centróide do triângulo.
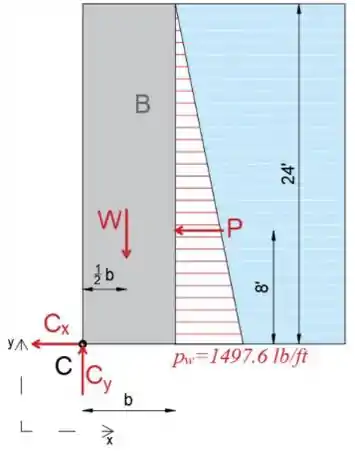
Equacionando a soma dos momentos sobre o ponto C a zero, determinaremos o peso necessário para resistir ao tombamento sobre C.
substitua e pelos valores calculados no passo acima.
Expressaremos a como:
Podemos calcular a quantidade de concreto necessária para resistir ao tombamento, colocando o valor de b na expressão (2)
Ao comparar os volumes necessários dos blocos A e B, podemos concluir que o bloco A exige menos concreto e calcularemos quanto.
Substitua e por seus valores.
Podemos expressar a diferença em concreto para os blocos A e B em peso multiplicando a diferença em ft³ pelo peso específico.
Resposta
O bloco A requer menos concreto.
a diferença de concreto expressa em volume
a diferença de concreto expressa em peso