Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 144
A barra esguia e uniforme do Prob. 6/41 é repetido aqui, mas agora o rolo ideal em B foi removido. O coeficiente de atrito estático em A é 0,70 e em B é 0,50. Determine o valor máximo do ângulo para o qual o equilíbrio é possível.
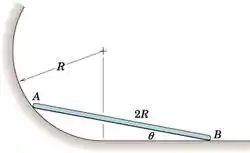
Passo 1
Primeiro, vamos isolar e desenhar o diagrama de corpo livre da barra AB
Podemos assumir com segurança que o ângulo será máximo quando ambas as forças de atrito em A e B são máximas
Conhecendo os coeficientes de atrito e , podemos determinar os ângulos e
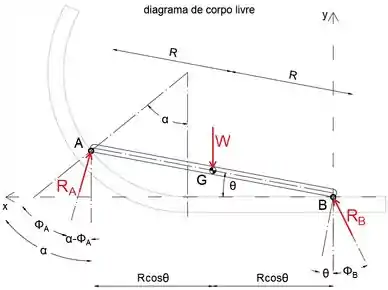
Passo 2
Ao igualar a soma dos momentos sobre o ponto A a zero, podemos escrever a força de reação RB como função do peso W
Podemos dividir os dois lados da equação por R
Substitua por seu valor
Passo 3
Ao igualar a soma das forças na direção x a zero, podemos escrever a força de reação FA como função do peso W
Substitua e por seus valores e RB pela expressão (1)
A partir daqui, podemos expressar RA como
Passo 4
Podemos notar que o ângulo desconhecido figura em ambas as expressões (2) e (3)
Deve ficar claro no esboço abaixo que
Finalmente, podemos escrever o ângulo como
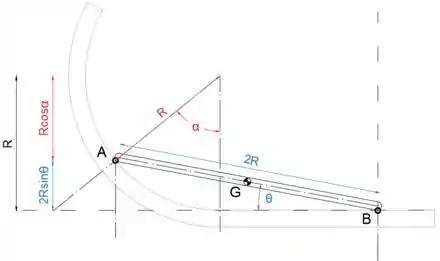
Passo 5
Podemos substituir pela expressão (4) nas equações (2) e (3), desta forma obteremos duas equações onde as únicas incógnitas são e RA
No esboço abaixo, é mostrado que quando o ponto A está em seu ponto mais alto, portanto, o ângulo máximo permitido é
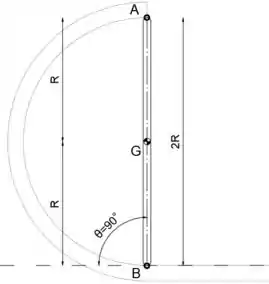
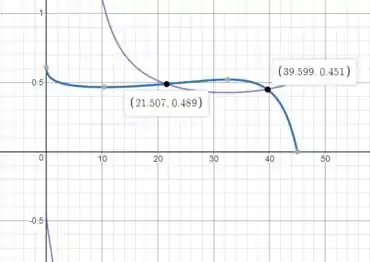
Passo 6
Usando uma calculadora gráfica como Desmo s (link nos comentários), representaremos as equações (5) e (6) no intervalo e leremos o ângulo que satisfaz ambas as equações do ponto de intersecção
Podemos ver que o sistema estará em equilíbrio para ambos
Portanto, podemos dizer que o ângulo máximo para o qual o sistema pode estar em equilíbrio é
