Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 64
O colar de é abandonado da posição mostrada e deixado cair sobre a blaca , que está fixa a uma barra de aço , de de diâmetro, e a duas outras barras de aço e , de de diâmetro. Sabendo-se que o tipo de aço usado apresenta e , determinar a maior distância admissível.
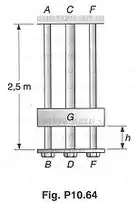
Passo 1
Como vocês estão, pessoas bonitas? Bora fazer uma questão de carregamento produzido por impacto pra você perceber que consegue arrasar em resistência dos materiais? Então bora!
Essa questão quer que a gente calcule a altura máxima que faz com que o colar transfira uma energia potencial às barras igual à máxima energia que elas suportam!
onde é a massa do colar, é a aceleração da gravidade e é a deformação das barras causada pelo impacto do colar.
Ainda não conhecemos o valor de deformação das barras . No entanto, todas as barras apresentam a mesma deformação por estaremos unidas. Podemos então calcular esse valor de deformação aplicando a Lei de Hooke em uma das duas barras finas iguais e .
onde é a máxima força que as barras mais finas e aguentam. Ela é calculada, multiplicando a tensão de resistência ao escoamento pela área da seção transversal de uma das barras ( ou ). Agora só falta achar para calcular . Esse valor é encontrado, somando as energias , e que cada barra é capaz de absorver.
onde é a máxima força que a barra do meio mais grossa aguenta. Ela é calculada, multiplicando a tensão pela área da seção transversal da barra .
A figura abaixo mostra os dados que temos para achar .
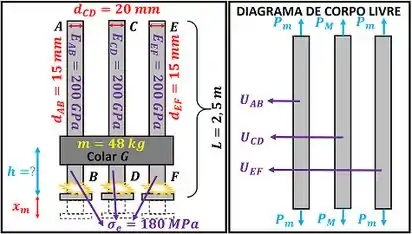
Com todas essas informações em mãos, vamos começar as contas.
Passo 2
Iniciamos os cálculos encontrando os valores de e .
Os dois são calculados multiplicando pela área da seção transversal de cada barra.
Logo, precisamos calcular as áreas , e antes de calcular as forças.
Para converter essas áreas de para , multiplicamos elas por .
Antes de calcular as forças, é necessário dizer que a tensão tem que ser convertida de para , multiplicando por .
Substituindo essas áreas nas equações de e , achamos:
Passo 3
Com e somos capazes de achar e pelas fórmulas abaixo.
No entanto, temos que nos ligar para converter , e de para , multiplicando esses três módulos de elasticidade por .
Substituindo na equação de , achamos:
Com esses dois termos, podemos achar no próximo passo.
Passo 4
Para achar é só substituir e na equação de do passo 1.
Boaaaaa! Achamos e terminamos a questão!