Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 98

A coluna de madeira tem seção transversal quadrada e consideramos que esteja acoplada por pinos no topo e na base. Se ela suportar uma carga axial de 250 kN, determine suas dimensões laterais a com aproximação de múltiplos de 10 mm. Use as fórmulas NFPA.

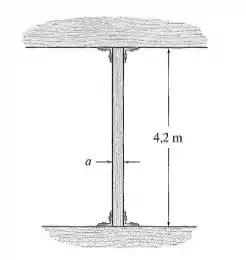
Passo 1

Como está acoplada por pinos nas extremidades,

Primeiramente, calculando-se o momento de inércia e a área, teremos:

Sabemos que a fórmula da tensão admissível é:

Isolando-se o e substituindo os outros dados, teremos:

Vamos agora verificar o índice de esbeltez:

Logo, vemos que não é maior que 26, logo, não serve.

Passo 2

Como o valor encontrado não foi compatível com a especificação, vamos calcular pela fórmula:

Isolando-se o , teremos:

Verificando o índice de esbeltez, teremos:

Logo, está ok.

O próximo múltiplo de 10 será

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

σ c = 8,3 M P a e um módulo de elasticidade ajustado E = 11,1G P a . Usando o método da tensão admissível, determine o maior comprimento de flambagem L admissível que pode ser usado.

σ c = 8,3 M P a e um módulo de elasticidade ajustado E = 11,1G P a . Usando o método da tensão admissível, determine o maior comprimento de flambagem L admissível que pode ser usado.10.100: Resolva o

E = 200 G P a e σ E = 250 M P a .

L 4 × 3 × 3 8 in. de aço são soldadas juntas de modo a formar a coluna AB. Uma carga axial P de intensidade 14kips é aplicada no ponto D. Utilizando o método das tensões admissíveis, determine o maior

10.108: Resolva o problema 10.107 considerando e = 40m m . b igual a 90 mm, 140 mm e 240 mm. Essa madeira tem uma tensão admissível ajustada à compressão paralela às fibras σ C = 8,1M P a e módulo de