Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 105

E = 200 G P a   e   σ E = 250 M P a .

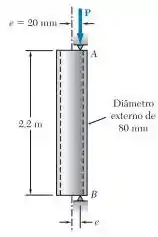
Passo 1

Então gurizada o enunciado pede que a gente determine o tubo mais leve que pode ser utilizado, vamos as equações que usaremos no passo 2 :D

r o = 1 2 d o = 40 m m ,

r i = r o - t

A = π r o 2 - r i 2 ,

I = π 4 r o 4 - r i 4

r = I A

Passo 2

Podemos determinar então a área, inercia, raio através das equações do passo 1 :D

L e = 2,2 m

P = 93 × 10 3 N

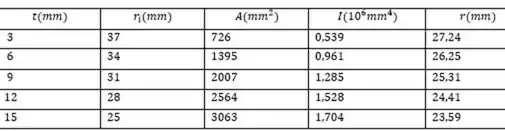
Transição L/r:

4,71 E σ γ = 4,71 200 × 10 9 250 × 10 6 = 133,22

Tente t = 9 m m ,

L e r = 2,2 25,31 × 10 - 3 = 86,92 < 133,22

σ e = π 2 E L e r 2 = π 2 200 × 10 9 86,92 2 = 261,27 M P a

σ a l l = σ c r 1,67 = 1 1,67 0,658 250 261,27 250 = 100,30 M P a

Passo 3

Temos então que:

P A + P e c I = 93 × 10 3 2007 × 10 - 6 + 93 × 10 3 20 × 10 - 3 40 × 10 - 3 1,285 × 10 - 6 = 104,2 M P a > 100,3 M P a

Área aproximado requerida

104,2 100,3 2007 = 2085 m m 2

Tente t = 12 m m .

L e r = 2,2 24,41 × 10 - 3 = 90,12 < 133,22

σ e = 243,05 M P a

σ a l l = 97,33 M P a

Passo 4

Temos então que:

P A + P e c I = 93 × 10 3 2564 × 10 - 6 + 93 × 10 3 20 × 10 - 3 40 × 10 - 3 1,528 × 10 - 6 = 85,0 M P a < 97,3 M P a

U s e   t = 12,00 m m

Resposta

12,00 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força axial de 53,4 k N é aplicada com uma excentricidade e = 9,53 m m à barra circular de aço BC que está livre no topo C e engastada na base B. Sabendo que o estoque de barras disponíveis para u
Cargas axiais de intensidade P = 600,5 k N são aplicadas paralelas ao eixo geométrico da coluna AB feita com um perfil de aço laminado W 250 × 80 e interceptam o eixo x a uma distância e do eixo geomé
Uma carga excêntrica em um ponto afastado 40m m do eixo geométrico de uma haste com 0,09m m de diâmetro feita de aço para qual α γ = 250M P a e E = 200G P a .Utilizando o método das admissíveis,determ
Um elemento de aço comprimido com comprimento de flambagem de 12f t suporta uma carga excêntrica conforme mostrado. Utilizando o método das tensões admissíveis, determine a excentricidade máxima admis
Uma carga excêntrica em um ponto afastado 22m m do eixo geométrico de uma haste com 60m m de diâmetro feita de aço para qual α γ = 250M P a e E = 200G P a .Utilizando o método das admissíveis,determin