Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 152

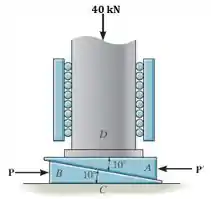
A coluna D está sujeita a uam carga vertical de 40   k N . Ela está suspensa em dois calços idênticos A e B para os quais o coeficiente de atrito estático nas superfícies de contato entre A e B e entre B e C é μ s = 0,4 . Determine a força P necessária para manter o calço A estacionário. A superfície de contato entre A e D é lisa.

Passo 1

De início, vamos dar uma olhada no diagrama de corpo livre do calço A para entendermos as forças que estão atuando.

Passo 2

Quando nós temos um sistema em equilíbrio, o somatório das forças que atuam nesse sistema, em todos os eixos de referência ( x , y , z ) é igual a zero. Vamos aplicar esse princípio na nossa questão! Adotando como direções positivas para cima e para direita, temos o seguinte:

∑ F y = 0

N c o s 10 ° - 0,4 N s e n 10 ° - 40000 = 0

N = 37,9   k N

∑ F x = 0

0,4 37,9 × 10 3 c o s 10 ° + 37,9 × 10 3 s e n 10 ° - P ' = 0

P ' = 21501,9   N

Passo 3

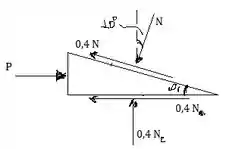
Vamos agora dar uma olhada no diagrama de corpo livre do calço B para entendermos as forças que estão atuando

Passo 4

Quando nós temos um sistema em equilíbrio, o somatório das forças que atuam nesse sistema, em todos os eixos de referência ( x , y , z ) é igual a zero. Vamos aplicar esse princípio na nossa questão! Adotando como direções positivas para cima e para direita, temos o seguinte:

∑ F y = 0

N c + 0,4 N s e n 10 ° - N c o s 10 ° = 0

N c + 0,4 37,9 × 10 3 s e n 10 ° - 37,9 × 10 3 c o s 10 ° = 0

N c = 34,7   k N

∑ F x = 0

P - 0,4 40 × 10 3 - 37,9 × 10 3 s e n 10 ° - 0,4 37,9 × 10 3 c o s 10 ° = 0

P = 37,5   k N

Resposta

A força P necessária para manter o calço A estacionário é igual a:

P = 37,5   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força P necessária para abaixar o cilindro de 80 lb do Prob. 6/81. Compare sua resposta com os resultados declarados desse problema. O valor sem atrito de P é igual à média das forças nece
Além da variação da pressão radial do Prob. 6/92, suponha que o coeficiente de atrito μ diminui linearmente com r de um valor μ0 no centro para μ0 / 2 em r = a. Derive uma expressão para o torque M ne
O carretel de cabo telefônico tem massa de 250 kg e é montado em um eixo de 80 mm de diâmetro. Se o coeficiente de atrito entre o eixo e seu rolamento for 0,30, calcule a tensão horizontal T necessári
Um torque M de 1510 N⋅m deve ser aplicado ao eixo de 50 mm de diâmetro do tambor de içamento para elevar a carga de 500 kg em velocidade constante. O tambor e o eixo juntos têm uma massa de 100 kg. Ca
O anel de aço A de 20 kg com raios interno e externo de 50 mm e 60 mm, respectivamente, repousa sobre um eixo horizontal fixo de raio de 40 mm. Se uma força descendente P = 150 N aplicada à periferia