Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 103

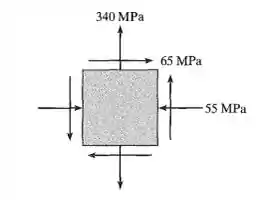
As componentes do estado plano de tensão em um ponto crítico sobre uma carcaça fina de aço são mostradas na figura. Determine se ocorre falha (escoamento) com base na teoria da tensão de cisalhamento máxima. A tensão de escoamento para o aço é σ e   =   650   M P a .

Passo 1

Fala aí galerinha. Este problema é bem simples. Primeiramente, vamos analisar as tensões dadas pelo problema. Sabemos que:

σ x = - 55 M P a

σ y = 340 M P a

τ x y = 65 M P a

O próximo passo é determinar as tensões principais, para que peguemos o caso mais crítico. Sabemos que as tensões principais são dadas por:

σ 1,2 = σ x + σ y 2 ± σ x - σ y 2 2 + τ x y 2

Substituindo, teremos:

σ 1 = 350,42 M P a

σ 2 = - 65,42 M P a

Passo 2

Agora é só aplicar a teoria da tensão de cisalhamento máxima. Para isso, vamos usar a fórmula abaixo:

σ 1 - σ 2 = σ e      

Temos que resolver o lado esquerdo da equação e verificar se este não ultrapassa o direito, pois haveria falha. Como:

416 < 650

Não haverá falha.

Resposta

Não haverá falha.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 10.69 usando a teoria da tensão de cisalhamento máxima. As duas tensões principais têm sinais opostos.
Resolva o Problema 10.71 usando a teoria da tensão de cisalhamento máxima. Ambas as tensões principais têm o mesmo sinal.
Se um eixo for feito de um material para o qual σ e = 350M P a , determine a tensão de cisalhamento por torção máxima exigida para provocar escoamento pela teoria da energia de distorção máxima.
A tensão de escoamento para um material plástico é σ e = 110M P a . Se esse material estiver sujeito ao estado plano de tensão e ocorrer uma falha elástica quando uma tensão principal for 120M P a , q
Um elemento diferencial é submetido à deformação no plano que tem as seguintes componentes: ∈ x = 950 × 10 - 6 , ∈ y = 420 × 10 - 6 ,γ x y = - 325 × 10 - 6 . Use as equações de transformação da deform