Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 47
A seção retangular da viga retangular é submetida a um momento M. Determine uma expressão para um aumento no comprimento das retas AB e CD. O material tem módulo de elasticidade E e coeficiente de Poisson
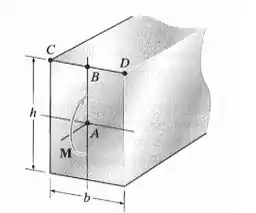
Passo 1
Fala aí galera. Este problema é pequeno mas a resolução dele é um pouco complexa, mas vamos lá.
Primeiramente, vamos determinar a tensão normal que atua em
Podemos substituir os valores da fórmula em função dos parâmetros dados, ficando com:
Agora, o próximo passo é calcular a deformação em
Podemos substituir a tensão pelo valor encontrado e ficaremos com:
Por fim, podemos calcular a variação AB pela integral abaixo:
Substituindo a expressão acima pelo valor encontrado e resolvendo a integral, teremos:
Passo 2
Agora, vamos fazer o mesmo para CD:
Calculando a deformação em
Logo, podemos achar a variação em CD:
Deixando claro que o nosso foco aqui não é treinar contas, mas a teoria. Logo, as operações foram simplificadas.