Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 126
O conjunto cabeçote-motor de uma furadeira radial de coluna estava originalmente posicionado com o braço paralelo ao eixo e com o eixo do mandril e da broca paralelo ao eixo . O conjunto foi, então, girado em torno do eixo e em torno da linha de centro do braço horizontal , trazendo-o para a posição mostrada na figura. O processo de furação teve início ligando-se o motor e girando-se as alavancas de ajuste para se colocar a broca em contato com a peça. Substitua a força e o binário exercido pela furadeira por um sistema força-binário equivalente ao centro da base da coluna vertical.
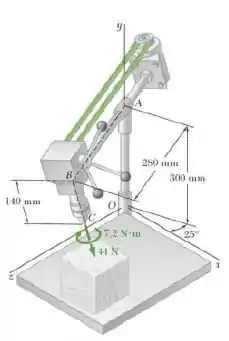
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Temos que a magnitude da força exercida pela broca é:
O binário exercido pela broca é dado por:
Vamos encontrar a força resultante e o momento resultante , equivalentes em relação ao ponto .
Para , temos:
Retratando o momento na forma vetorial, temos:
Passo 2
Para o cálculo do momento resultante em , precisamos calcular os vetores deslocamentos. Para cada ponto em que exista uma força aplicada, existirá um vetor deslocamento com origem em e fim no ponto de aplicação, portanto:
Agora, podemos calcular o momento resultante em , através do produtor vetorial do vetor deslocamento e das forças. Temos que:
Logo:
Resolvendo, temos: