Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 42
Para o bloco dos Problemas 2.37 e 2.38, determine (a) o valor necessário de para que o resultante das três forças mostradas seja paralela ao plano inclinado, (b) a correspondente intensidade da resultante.
Passo 1
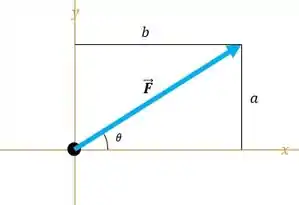
Bom galera, a gente vai encontrar as componentes horizontais e verticais de cada uma das forças que é dada por:
Passo 2
Show de bola, a gente sabe que a resultante será paralela ao plano inclinado, então vamos considaderar o plano inclinadoo no eixo , então a resultante no eixo será :
Pela propriedade da trigonometria:
Então substituindo, temos:
Usando a função inversa da tangente na calculadora, assim encontramos:
Passo 3
Por último, a gente calcular a soma das componentes paralelas ao plano inclinado, porque a resultante atuará apenas nesse eixo:
Resposta
Exercícios de Livros Relacionados
A força de 180l b é aplicada no ponto A do suporte. Determine os momentos desta força sobre o ponto B, sobre o ponto C e sobre a linha B C - .
Substitua as duas forças e o binário simples por um sistema de força-binário equivalente no ponto A.
O topo horizontal de um pilar de concreto está sujeito ao sistema de forças mostrado. Represente a resultante de todas as forças como uma força R → no ponto O e um binário M → . Também especifique as
Duas cargas ascendentes são exercidas na pequena treliça tridimensional. Reduza essas duas cargas a um único sistema de força-binário no ponto O. Mostre que R → é perpendicular a M O → . Em seguida, d
Ao apertar um parafuso cujo centro está no ponto O, a pessoa exerce uma força de 40l b na alavanca da catraca com a mão direita. Além disso, com a mão esquerda, ele exerce uma força de 20l b , conform