Construa os diagramas de cortante e de momento para a viga carregada mostrada. Determine o momento fletor máximo e sua posição.

Passo 1
Para calcular a força cortante e o momento fletor na viga, fazemos um corte na coordenada a partir de e isolamos em diagrama de corpo livre a parte esquerda da viga. Calculamos a força e o momento resultantes causados pela distribuição de forças no trecho e assim determinamos e aplicando as condições de equilíbrio.
Passo 2
Primeiro vamos determinar a intensidade de forças que atua na viga. Temos no ponto de coordenada a partir de uma intensidade de 2,4 kN/m:
Para m temos uma intensidade de 4,8 kN/m:
Tendo o valor da intensidade , conseguimos determinar a força de reação em , que precisamos pois ela atua na parte esquerda da viga que isolaremos. Vamos calcular o momento total feito pela distribuição de forças no ponto , e então obter fazendo a soma dos momentos em torno de ser zero. A força causada em um elemento de espessura é:
Esse elemento se situa a uma distância de do ponto , então o momento causado em torno do ponto é:
Vamos então integrar de 0 a para encontrar o momento total em torno de causado pela distribuição de forças:
A força de apoio em é então obtida pela soma dos momentos em torno de :
Passo 3
Então isolamos em diagrama de corpo livre a parte à esquerda de um corte feito a m de :
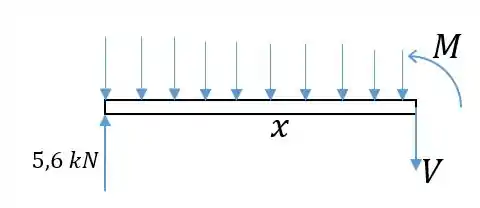
Passo 4
Precisamos calcular a força resultante causada pela distribuição de forças nesse trecho para encontrar . A força causada em um elemento de espessura de coordenada é:
Note que agora é considerado uma constante, pois é o tamanho do nosso trecho. O que varia é a quantidade que chamamos de , que vai de 0 a . Então integramos:
Pelo equilíbrio das forças verticais, achamos então :
Passo 5
Agora para encontrar precisamos do momento resultante causado pela distribuição de forças em torno do ponto de coordenada . Sabemos que a força causada num elemento é:
A distância desse elemento até a coordenada da viga é:
Então temos:
Lembrando que é uma constante! Integramos então de 0 a :
Então obtemos fazendo ser zero o momento em torno da seção de coordenada :
Passo 6
Tendo então as funções e , representamos graficamente os diagramas de cortante e de momento:
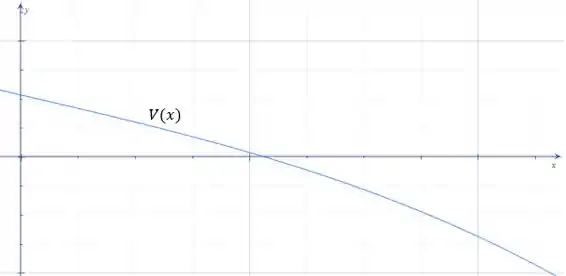

Fazendo uma análise do gráfico descobrimos o momento fletor máximo:
Resposta

