Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas fundamentais - Ex. 4
Determine a força normal, o esforço cortante e o momento no ponto .
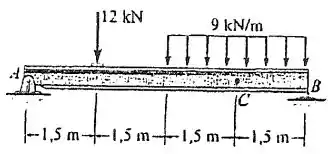
Passo 1
Fala! Ele quer os esforços internos na seção
Para achar os esforços internos nessa viga biapoiada, temos um passo a passo
- achar a reações em um dos apoios (no nosso caso, ajuda se for o apoio mais perto da nossa seção.
- cortar a viga na seção desejada e olhar só para o lado onde as forças são conhecidas
- posicionar os esforços e acha-los pelas equações de equilíbrio
Além disso, como há uma carga distribuída deve-se determinar a força resultante gerada por essa carga e a sua posição. Logo, como a carga é retangular, a força resultante é dada por:
E a sua posição é:
Dito isso tudo, bora começar!
Passo 2
Então, primeiramente, fazendo o diagrama de corpo livre de todo o sistema:
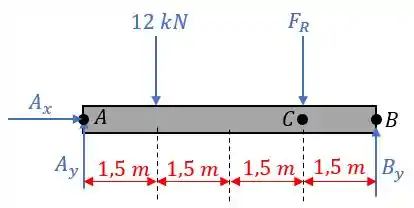
É possível encontrar a reação exercida no ponto de apoio, tal que, como o ponto possui duas variáveis, elas devem ser “eliminadas” do cálculo para que não haja mais variáveis do que o número de equações.
Para isso acontecer, vamos aplicar o princípio dos momentos para o ponto e considerar que o momento seja positivo no sentido anti-horário. Então:
Tal que:
Isolando :
Passo 3
Vamos cortar nossa viga em e olhar para a direita, onde todas as forças são conhecidas. Aí a gente posiciona os esforços internos em seguindo a convenção positiva. E vamos acha-los pelas equações de equilíbrio.
Logo, fazendo o DCL dessa seção e mostrando as forças e reações aplicadas, teremos:
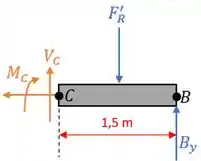
Como o comprimento da seção diminuiu, a força resultante exercida pela carga distribuída e a sua posição também se alteram.
Continuamos com , mas agora o comprimento da viga é de . Então, teremos que:
E:
Agora, fazendo o equilíbrio de forças em obtém-se:
Fazendo o equilíbrio de forças em :
Tal que:
Isolando a força cortante:
Passo 4
E aplicando o princípio dos momentos no ponto , considerando que o momento é positivo no sentido anti-horário, é possível ter:
Isso nos dá:
Portanto:
E então:
O sinal negativo indica que o esforço cortante atua no sentido oposto, ou seja, no sentido para baixo.
Resposta