Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 48

Duas cunhas de 8° e massa desprezível são usadas para mover e posicionar um bloco de 800 kg. Sabendo que o coeficiente de atrito estático em todas as superfícies de contato é 0,30, determine a menor força P que podera ser aplicada, como mostrado na figura, em uma das cunhas.

Passo 1

Tá legal! Vamos começar esse excercício desenhando o diagrama de corpo livre para o bloco e a cunha da direita:

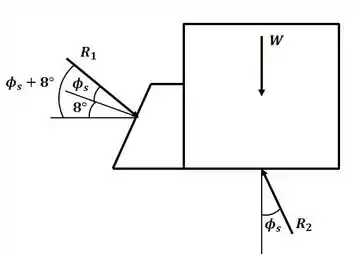
Conforme vimos na seção anterior do livro, o coeficiente de atrito pode ser encontrado através de:

Substituindo o valor dado de :

Passo 2

Agora, podemos desenhar o triângulo de forças para o sistema anterior:

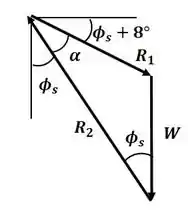
Agora, por trigonometria, podemos descobrir o valor de :

Agora, aplicando a lei dos senos para o triângulo de forças, temos:

Passo 3

Agora vamos analisar o desenhar o diagrama de corpo livre para a cunha da esquerda:

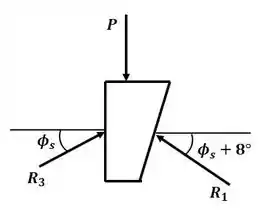
E, com esse DCL, podemos montar o triângulo de forças a seguir:

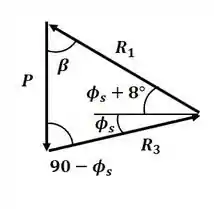
Agora vamos aplicar a lei dos senos para esse triângulo:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força de fixação exercida no bloco se uma força P = 30N é aplicada na manivela da morsa. O parafuso de rosca quadrada simples tem um diâmetro médio de 25m m e um passo de 7,5m m . O coefic

O dispositivo é usado para puxar o terminal de cabo de bateria C do contato de uma bateria. Se a força de puxada necessária é 425N , determine o torque M que precisa ser aplicada ao cabo do parafuso p

O mecanismo de elevação consiste em um conjunto que tem um parafuso com rosca quadrada com diâmetro médio de 12m m e um passo de 5m m , e o coeficiente de atrito estático é μ s = 0,4 . Determine o tor

Determine a menor força vertical P exigida para empurrar o calço entre os dois cilindros idênticos, cada um com peso W . O coeficiente de atrito estático em todas as superfícies de contato é μ s = 0 ,

Se aforça horizontal P for removida, determine o maior ângulo θ que fará com que a cunha seja autotravante, independente da intensidade da força F aplicada à alavanca. O coeficiente de atrito estático