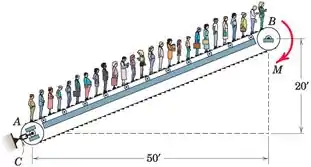
A correia sem fim de uma escada rolante passa ao redor do tambor intermediário A e é impulsionada por um torque M aplicado ao tambor B. A tensão da correia é ajustada por um tensor em C, que produz uma tensão inicial de 1000 libras em cada lado da correia quando a escada rolante é descarregada. Para o projeto deste sistema, calcule o coeficiente mínimo de atrito m entre o tambor B e a correia para evitar escorregamento se a escada rolante mantiver 30 pessoas uniformemente distribuídas ao longo da correia e com média de 150 lb cada. (Nota: pode ser mostrado que o aumento na tensão da correia no lado superior do tambor B e a diminuição na tensão da correia no tambor inferior A são cada uma igual à metade do componente do peso do passageiro combinado ao longo da inclinação.)

Sabemos que a tensão da correia é inicialmente T = 1000 lb e que a tensão no lado superior é aumentada pela metade do componente de peso do passageiro Wn, enquanto a tensão no lado inferior é diminuída como mostrado no esboço

Uma vez que o componente de peso ao longo da inclinação é

Onde 0 é o ângulo de inclinação

Podemos determinar o componente Wn

Uma vez que determinamos o componente Wn, podemos determinar as tensões da correia no ponto B