Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 137

Uma corda uniforme de 1250   m m de comprimento passa por uma roldana em B e é fixada em um pino de apoio em A . Sabendo que L = 500   m m e desprezando o efeito do atrito, determine o menor dos dois valores de h para que a corda esteja em equilibrio.

Passo 1

Bom galera, vamos fazer um diagraminha de corpo livre, só pra facilitar nossa vida:

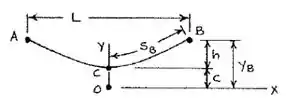
Com isso, de cara a gente já tem alguns valores:

x B = 500 2 = 250   m m

b = 1250 - 2 s B

T m = T B = w b = w ( 1250 - 2 s B )

Passo 2

Show de bola, agora a gente pode usar a equação 7.15 :

s B = c sinh ⁡ x B c

E a equação 7.16 :

y B = c cosh ⁡ x B c

Agora a gente usar a equação da tensão máxima:

T m = w y B

→ w 1250 - 2 s B = w c cosh ⁡ x B c

→ 1250 - 2 c sinh ⁡ x B c = c cosh ⁡ x B c

→ 1250 - 2 c sinh ⁡ 250 c = c cosh ⁡ 250 c

Resolvendo isso a gente pode encontrar dois valores para c :

c = 138,725   m m

c = 693,55   m m

Passo 3

Calma, tá quase acabando. Vamos usar calcular os dois valores que podem fica h para cada c :

Para c = 138,725   m m :

y B = h + c

→ 138,725 ⋅ cosh ⁡ 250 138,725 = h + 138,725

→ h = 293,2   m m

Agora, só trocamos c por 693,55   m m , ai encontraremos:

h = 45,5475   m m

Resposta

h = 293,2   m m

h = 45,5475   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilizando o método da seção 7.6, resolva o problema 7.33.
Utilizando o método da seção 7.6, resolva o problema 7.31.
Utilizando o método da seção 7.6, resolva o problema 7.34.
Para o carregamento mostrado, (a) trace os diagramas de esforço cortante e momento fletor e (b) determine os valores absolutos máximos de momento e de cortante.
Utilizando o método da seção 7.6, resolva o problema 7.30.