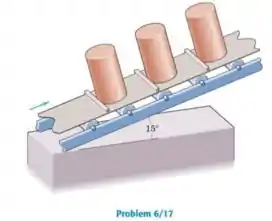
Uma correia transportadora com calços leva cilindros sólidos homogêneos para cima em uma inclinação de 15°. O diâmetro de cada cilindro é metade de sua altura. Determine a aceleração máxima que a correia pode ter sem derrubar os cilindros na partida.

Bom, os cilindros se deslocam com uma aceleração no sentido de subida da correia, para a direita conforme o desenho do enunciado, vamos então imaginar uma observação exatamente pela lateral do cilindro, ele terá a aparência de um retângulo, onde o diâmetro seria o lado menor e a altura o lado maior:

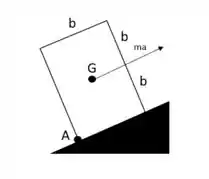
O ponto A que será o objeto de nosso interesse, vamos escrever a equação do momento para esse ponto:

Onde d será a distância de A até a linha que passa sobre o vetor , ou seja b.

Os momentos envolvidos serão causados pelas componentes da força peso:

Devido ao ângulo da correia com a horizontal