Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 16
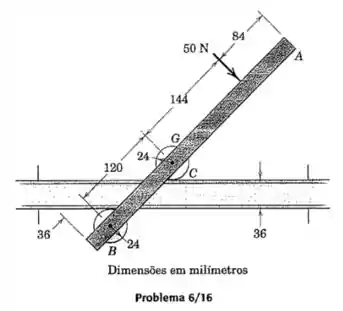
Um dispositivo consiste na barra uniforme de com dois cilindros leves que aplicam força aos laminados na parte superior e na parte inferior de uma bancada. Determine a força exercida por cada cilindro sobre o laminado quando uma força de 50N é aplicada perpendicular à barra na posição indicada. Despreze qualquer atrito.
Passo 1
Para esse problema, vamos utilizar um ponto D que está fora do corpo da barra, de maneira que fique na mesma linha horizontal que passa pelo centro de massa G e na mesma linha vertical que passa pelo ponto C, conforme a figura:
A força exercida sobre o laminado por cada cilindro será de igual em modulo que a força exercida sobre os cilindros, por isso as setas apontam para o dispositivo.
Como podemos perceber, a equação dos momentos para D será igual a zero pois a linha do vetor passa por ele. Além disso, o momento de da força sobre o ponto C não irá ser incluído na equação pelo mesmo motivo.
Passo 2
Vamos então escrever a equação dos momentos em relação ao ponto D:
Que será:
Onde é a distância da força aplicada dada no enunciado, é a distância do ponto B até a vertical que liga C e D, e será o ângulo formado entre o dispositivo e a horizontal
Calculando a distância do centro de massa:
E a distância da força até D:
Isolando e resolvendo:
Passo 3
Para encontrarmos a força sobre C, vamos usar a segunda lei de Newton, já que agora temos a força sobre B, não há aceleração nessa direção x, então:
Isolando :
Resolvendo: