Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 8

Na posição de equilibro, o cilindro de 30 kg provoca uma deflexão estática de 50 mm na mola helicoidal. Se o cilindro é abaixo um adicional de 25 mm e liberado a partir do repouso, calcule a frequência natural resultante da vibração vertical do cilindro em ciclos por segundo (Hz).

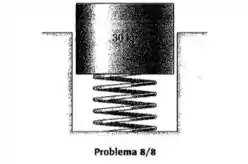
Passo 1

Primeiro vamos usar a deflexão da mola antes de ela ser abaixada mais 25 mm para calcularmos a constante elástica através do peso do cilindro, pela segunda lei de Newton:

Isolando k:

E substituindo os valores das grandezas:

Passo 2

E então utilizamos a equação da frequência angular para o caso em que a mola foi abaixada mais 25 mm e que passa a oscilar para obtermos a equação em Hertz, pois agora temos o valor da constante elástica:

Substituindo uma na outra:

Isolando :

E substituindo os valores de cada grandeza:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um oscilador harmônico amortecido é formado por um bloco ( m = 2,00k g ), uma mola ( k = 10,0N / m ) e uma força de amortecimento ( F = - b v ). Inicialmente, o bloco oscila com uma amplitude de 25,0c

A Amplitude de um oscilador fracamente amortecido diminui de 3,0 % a cada ciclo. Que percentagem da energia mecânica do oscilador é perdida em cada ciclo?

Em um oscilador amortecido com m = 250 g , k = 85 N / m e b = 70 g / s , qual é a razão entre a amplitude das oscilações amortecidas e a amplitude inicial após 20 ciclos?

O sistema de suspensão de um automóvel de 2000 k g “cede” 10 c m quando o chassis é colocado no lugar. Além disso, a amplitude das oscilações diminui de 50 % a cada ciclo. Estime o valor (a) da consta

Na Fig 15-14 o bloco possui uma massa de 1,50 k g e a constante elástica é 8,00 N / m . A força de amortecimento é dada por - b d x / d t , onde b = 230 g / s . O bloco é puxado 12,0 c m para baixo e