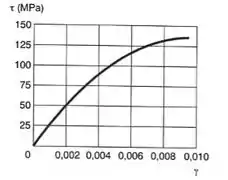
A curva mostrada na e pode ser aproximada pela relação:

Usando esta relação e as equações (3.2) e (3.26) resolver o problema indicado.

Pelos dados que o enunciado nos dá temos que:

E as equações que o enunciado menciona são dadas por:

• Equação (3.2)
• Equação (3.26)

Sabemos que a fórmula da nossa deformação especifica cisalhante é dada por:

E podemos definir uma razão Z pela seguinte fórmula:

Mas poque marcamos isso? Porque sabemos que a nossa fórmula para determinação do torque, quando temos uma curva indefinida, é dada pela fórmula 3.26:

Se colocarmos a nossa razão Z na equação, teremos a seguinte relação:

Substituindo na equação teremos que:

Que na equação passará a ser:

Agora a nossa variável passa a ser Z, sendo assim teremos que mudar a variável, e basta derivarmos a seguinte equação.

Substituindo teremos que:

Lembrando que é a variação do raio, e que C é o raio máximo, então sabemos que a razão

Varia entre 0 e 1, sendo assim podemos mudar a variação da integral que para variava de 0 até C, sendo assim teremos que:

Sabemos que o enunciado já nos dá uma equação, mas que podemos escrever o seguinte:

Como temos uma equação dada por:

Podemos escrever a seguinte equação:

Substituindo na nossa equação da tensão cisalhante teremos que:

Como no nosso enunciado temos uma equação de tensão cisalhante, podemos comparar as duas da seguinte maneira:

Substituindo na nossa integral teremos que:

Sabemos que: