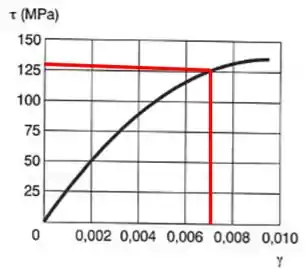
Um eixo vazado de diâmetro interno e externo iguais a , respectivamente, é fabricado de uma liga de alumínio, cujo diagrama é mostrado. Determinar:

1. O torque necessário para torcer um eixo de de comprimento, de um ângulo de 10°.
2. O correspondente valor da máxima tensão de cisalhamento.

Pelos dados que o enunciado nos dá temos que:

Com isso podemos determinar as máximas deformações especificas cisalhantes, com isso teremos que:

Sabemos que a fórmula da nossa deformação especifica cisalhante é dada por:

E podemos definir uma razão Z pela seguinte fórmula:

E também podemos escrever essa fórmula da seguinte maneira:

Mas poque marcamos isso? Porque sabemos que a nossa fórmula para determinação do torque, quando temos uma curva indefinida, é dada pela seguinte fórmula:

Se colocarmos a nossa razão Z na equação, teremos a seguinte relação:

Substituindo na equação teremos que:

Que na equação passará a ser:

Agora a nossa variável passa a ser Z, sendo assim teremos que mudar a variável, e basta derivarmos a seguinte equação.

Substituindo teremos que:

Lembrando que é a variação do raio até o raio , e que a variação do fator Z é feito da seguinte maneira:

Se dividirmos as variações da integral por , teremos que:

E já sabemos que pelo cálculo que fizemos antes temos que:

Assim teremos que:

E podemos definir que:

Que simplificando a equação teremos que:

Porém, vou te ensinar um macete, resolver a nossa integral seria muito complicado, além do mais, não conhecemos a nossa curva, e não sabemos a sua fórmula, por isso podemos macetear a nossa integral usando um conceito de solução numérica, ou seja, vamos usar uma solução aproximada para o nosso problema, e com isso usaremos um conceito de fórmula de Simpson para isso. Não vale apena entendermos todo o processo para chegar nela, até porque isso seria mais uma questão inteira a ser resolvida, mas como um passe de magica podemos aceitar que a nossa integral pode ser simplificada de seguinte maneira.

Sabemos que é de quanto em quanto queremos que o nosso fator Z seja analisado, sabemos que Z varia de até 1, então para facilitarmos, vamos definir que a variação vai ser feita pelo seguinte valor:

Outra coisa que precisamos saber antes de continuar é que o W são fatores de multiplicação que valem o seguinte:

Sendo assim podemos montar uma tabela que será dada por:

Para determinarmos a deformação, e em seguida determinarmos as tensões, devemos usar a seguinte relação:

Em que sabemos que:

Substituindo para cada um dos itens teremos que:

E agora podemos determinar o resto da tabela, a partir das deformações, podemos determinar as tensões da seguinte maneira.

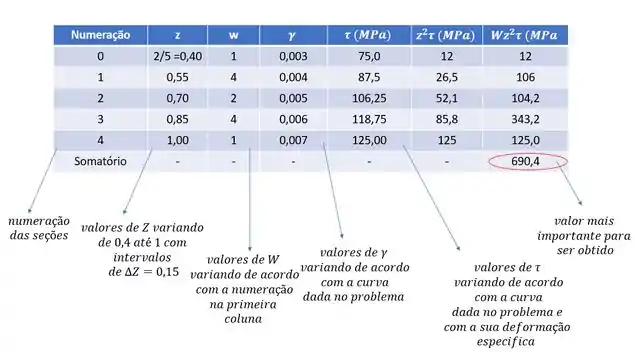
Vale lembrar que a nossa fórmula de Simpson é dada pela seguinte equação:

E o que acabamos de determinar foi:

Substituindo tudo teremos que:

E depois disso tudo conseguimos enfim determinar o nosso item A), que é exatamente o valor do nosso torque: