Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 141b
As deformações abaixo foram determinadas na superfície da base de uma máquina de ferro fundido. Sabendo-se que e , determinar os planos principais e as tensões principais: (a) pela determinação do correspondente estado plano de tensões. (Usar Eq. (2.36); Eq(2.43); e as duas primeiras equações do Prob. 2.76); e então, usar o círculo de Mohr para tensões; (b) Usando o círculo das deformações principais; e então, determinar as correspondentes tensões.
Passo 1
Para resolver este problema nós primeiro temos de calcular o coeficiente de Poisson pela equação. Depois a gente vai aplicar a equação da tensão normal de modo a desenhar o ciclo de Mohr como pedido.
Por fim iremos fazer o ciclo de mohr para as deformações.
Passo 2
Para achar o coeficiente de Poisson a gente vai utilizar a equação:
Dessa forma:
Passo 3
Vamos fazer então o ciclo de Mohr para deformações. Para isso a gente tem que lembrar como calcula a deformação específica normal média e o raio:
Perceba que é muito parecido com o ciclo de Mohr com as tensões mas aqui utilizamos:
- que é a deformação específica normal.
- que é a deformação angular.
utilizando os cálculos do passo 1:
E
Agora podemos desenhar o ciclo de Mohr:
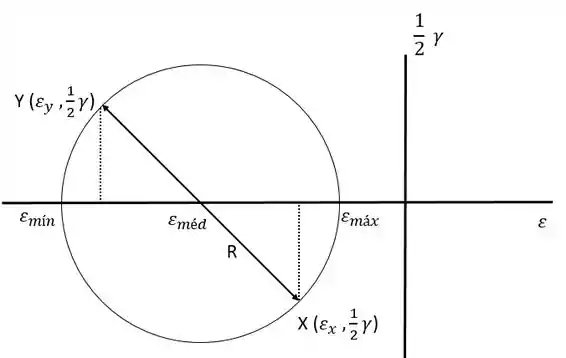
Passo 4
Para calcular a intensidade dessas deformações específicas normais principais temos que calcular e . Como já temos a média o o raio fica fácil:
Passo 5
Agora podemos achar o ângulo por meio da geometria do círculo de Mohr:
Para achar o outro plano basta adicionar 90°
Passo 6
Por fim para a gente achar as tensões devemos substituir na equação que relaciona tensão com deformação (lembrando que a gente calculou la no começo):
Para
Como trata-se de um estado plano de tensões temos que
Resposta
b)