Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 147
Para a barra do Prob. 6.146, determinar a leitura que poderia ser obtida para vários carregamentos, se o extensômetro estivesse localizado em um ponto diretamente acima, distante do ponto , e com a mesma orientação.
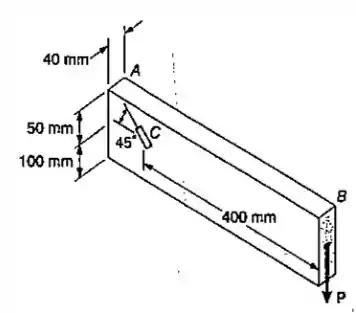
Passo 1
Para essa questão a gente tem que observar que, no ponto dado, existe apenas a tensão cisalhante, ou seja toda a deformação da roseta é angular.
Além disso foram fornecidos os dados e . Isso nos permite calcular a resistência à torção , que iremos calcular no passo 2, mas já vou deixar a equação aqui pra vocês:
Finalmente a gente vai ter que calcular a tensão de cisalhamento e para isso a gente vai usar a nossa boa e velha “tau vê Q i t”
partiu então!
Passo 2
Como dito vamos calcular a resistência à torção :
Passo 3
Agora vamos calcular a tensão de cisalhamento que a força gera na barra:
O perfil da nossa barra:
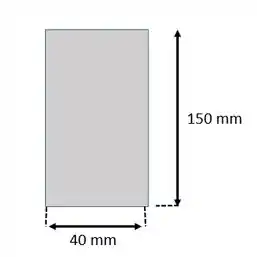
Então a gente tem que calcular o momento de inércia que para uma barra é dado por:
Agora o momento , aqui a gente tem que analisar onde a roseta está posicionada na peça:
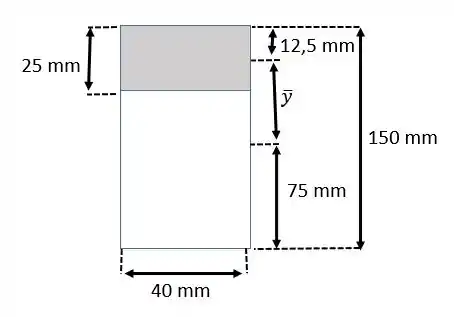
O momento é calculado como:
Agora a gente tem que achar que é a distância entre o centroide da peça como um todo e o centroide da parte superior apenas:
Pronto, agora é só substituir:
Ufa! Agora é só substituir na equação da tensão:
Lembrando que é a espessura e a força cortante que no caso vale :
Passo 4
Finalmente baste substituir na equação da deformação angular:
Se a gente supor um carregamento de , vamos ter: