Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 86

Um eixo de diâmetro 45mm é feito de um aço com 250MPa de resistência ao escoamento na tração. Usando o critério da máxima energia de distorção, determinar a intensidade da força P, para que o início do escoamento ocorra quando T= 1,7kN.m.

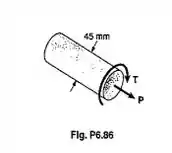
Passo 1

Fala aí, vem comigo matar essa questão de critérios de falha?

Vamos começar analisando o que a gente tem e reunindo as equações que vamos precisar:

Temos um esforço de torção que causa tensão cisalhante, e um esforço normal de tração que vai causar tensão normal.

σ x = P A

τ = T c J

Passo 2

Bom, agora bora calcular as propriedades geométricas da nossa peça pois serão necessárias pro cálculo das tensões.

A = π d 2 4 = 1590,43 m m ²

c = r = 45 2 = 22,5 m m

J = π r 4 2 = 402,578 × 10 3 m m 4

Passo 3

Agora voltamos nas equações de tensão e substituindo:

τ = 1,7 × 10 3 × 1000 × 22,5 402,578 × 10 3

τ = 95,01 M P a

Enquanto não temos o valor de P, vamos manter a tensão dessa forma o que vai economizar algumas contas pra gente.

σ x = P A

Se liga aqui! Precisamos encontrar os planos principais pra gente trabalhar com o nosso critério.

c = σ x + σ y 2 = - P 2 A

c = σ x 2

R = σ x 2 2 + τ ²

E as tensões principais são.

σ 1 = c + r

σ 2 = c - r

Passo 4

O critério da máxima energia de distorção diz que:

σ e 2 = σ 1 2 + σ 2 2 - σ 1 σ 2

E substituindo, a gente vai ter:

250 2 = c + r 2 + c - r 2 - ( c + r ) ( c - r )

62500 = c 2 + 2 r + r 2 + c 2 - 2 r + r 2 - c 2 + r 2

62500 = 3 r 2 + c 2

62500 = σ x 2 4 + 3 σ x 2 4 + τ 2

62500 - τ 2 = σ x 2

Enfim, substituindo de novo:

σ x = 62500 - 3 × 95,01 2 = 73,62 M P a

E enfim:

P = σ x A = 73,62 × 1590,43

P = 117,01 × 10 ³ N

P = 117,01 k N

Resposta

P = 117,01 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cabo fino que se encontra ao longo do eixo x é deformado de tal modo que cada um de seus pontos sofre um deslocamento ∆ x = k x ² ²ao longo do eixo. Se k for constante, qual a deformação normal em
O bloco é deformado até chegar à posição mostrada pelas linhas tracejadas. Determine a deformação normal média ao longo da reta AB.
A chapa retangular é submetida à deformação mostrada pela linha tracejada. Determine a deformação por cisalhamento média γ x y na chapa.
A forma original de uma peça de plástico é retangular. Determine a deformação normal média que ocorrer ao longo das diagonais AC e DB.
O quadrado deforma-se até chegar à posição mostrada pelas linhas tracejadas. Determine a deformação por cisalhamento em cada um de seus cantos A, B, C e D. O lado D’B’ permanece horizontal.