Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 24
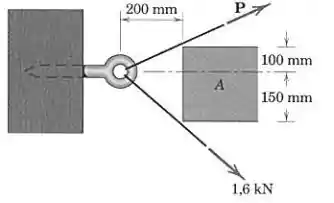
Deseja-se remover o pino da madeira pela aplicação de uma força ao longo de seu eixo horizontal. Um obstáculo impede um acesso direto, de modo que duas forças, uma de e a outra , são aplicadas por cabos, como mostrado. Calcule o módulo de necessário para assegurar uma resultante direcionada ao longo do pino. Determine também o valor de .
Passo 1
Na figura a seguir, representamos todas as forças, incluindo a resultante horizontal :
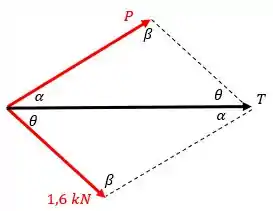
Para determinar cada um dos ângulos, observamos as dimensões dada na figura do enunciado:
Passo 2
Show! Agora, com base na figura, usamos a lei dos senos para determinar o módulo :
Para determinar o módulo , podemos novamente utilizar a lei dos senos:
Resposta
Exercícios de Livros Relacionados
204- A determinação exata da posição vertical do centro de massa G de um navio é difícil de ser obtida por cálculo. Ela é mais facilmente obtida por um experimento simples de inclinação do navio carre
2.45. Se a força resultante que atua sobre o suporte precisa ser direcionada ao longo do eixo x positivo e a intensidade de F 1 precisa ser mínima, determine as intensidades da força resultante e de F
O elemento B D exerce sobre o elemento A B C uma força P dirigida ao longo da linha B D . Sabendo que P deve ter um componente horizontal de 1330N , determine (a) a intensidade da força P , (b) sua co
Determine os componentes x e y de cada uma das forças indicadas.
Determine a resultante das três forças do Problema 2.24.