Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 5

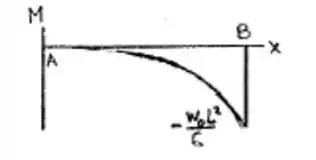
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado.

Passo 1

Como não temos nenhuma força nova no decorrer da barra, podemos admitir que o x vai ser válido para toda a barar, ou seja, de 0 a L.

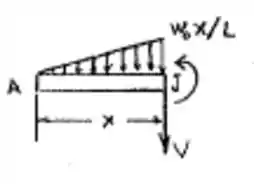
Pra facilitar nossa vida, podemos trocar a força distribuída por uma força pontual. Fazemos então

Vamos então fazer a análise das forças para montarmos o diagrama de forças cortantes. Vou adotar as forças pra cima como positivas.

Agora podemos ver como vai ser em x=L

O gráfio então fica

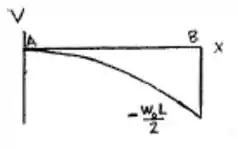
Passo 2

Fazemos agora a mesma análise para o momento e montamos o diagrama de momento fletor. Adotaremos o sentido anti-horário como o positivo.

Sabemos que na extremidade B é onde teremos o maior momento em módulo...

Podemos entçao montar o diagrama

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o estado plano de tensões mostrado, determinar a máxima tensão de τ x y para que a máxima tensão de cisalhamento seja de: (a) 6 0M P a ; (b) 78M P a .

Para o estado plano de tensões mostrado, determinar a máxima tensão de cisalhamento, quando: (a) σ x = 140M P a e σ y = 70M P a ; (b) σ x = 85M P a e σ y = 35M P a .

Para o estado plano de tensões mostrado, determinar a máxima tensão de cisalhamento, quando: (a) τ y z = 120M P a ; (b) τ y z = 55M P a ; (c) τ y z = 0 .

Para o estado de tensões dado, determinar as tensões, normais e de cisalhamento, exercidas sobre a face obliqua do triângulo sombreado do elemento. Usar o método de análise baseado nas equações de equ

Para o estado de tensões dado, determinar as tensões, normais e de cisalhamento, exercidas sobre a face obliqua do triângulo sombreado do elemento. Usar o método de análise baseado nas equações de equ