Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 3

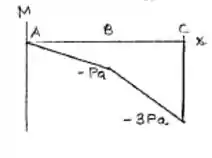
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado.

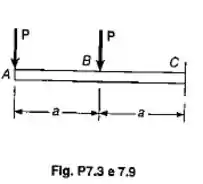
Passo 1

Para x de zero até a.

0 < x < a

Vamos então fazer a análise das forças para montarmos o diagrama de forças cortantes. Vou adotar as forças pra cima como positivas.

Σ F = 0 → - P - V = 0 → V = - P

Observe que temos V como uma constante.

Analisando o momento para esse intervalo de x variando entre 0 e a. (Anti-horário positivo)

Σ M = 0 → M + P x = 0 → M = - P x

Passo 2

Vamos refazer essa análise, só que agora com nosso x variando entre a e 2a

a < x < 2 a

Fazendo as forças para cima como sentido positivo para a análise do cortante e o sentido anti-horário como positivo para análise do momento.

Σ F = 0 → - P - P - V = 0 → V = - 2 P

Σ M = 0 → P x + P x - a + M = 0 → M = - 2 P x + P a

Passo 3

Sabemos que o V é constante entre 0 e a, e entre a e L, ficamos então com

Para o diagrama do momento que vamos calcular, sabemos os pontos onde vamos ter uma mudança no momento é no ponto a.

M x = - P x

M a = - P a

Para o momento final vamos calcular no ponto C, ou seja, x=2a

M x = - 2 P x + P a

M 2 a = - 2 P 2 a + P a = - 4 P a + P a = - 3 P a

Resposta

M m í n = - 3 P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o estado de tensões dado, determinar: (a) a orientação dos planos de máxima tensão de cisalhamento, no plano; (b) a tensão cisalhante máxima (c) a correspondente tensão normal.
Para o estado de tensões dado, determinar as tensões, normal e de cisalhamento, depois que o elemento mostrado tenha sofrido uma rotação de: (a) 40°, no sentido anti-horário; (b) 15°, no sentido horár
Para o estado de tensões dado, determinar as tensões, normal e de cisalhamento, depois que o elemento mostrado tenha sofrido uma rotação de: (a) 40°, no sentido anti-horário; (b) 15°, no sentido horár
Para o estado plano de tensões mostrado, determinar a máxima tensão de τ x y para que a máxima tensão de cisalhamento seja de: (a) 7 0M P a ; (b) 60M P a .
Para o estado plano de tensões mostrado, determinar a máxima tensão de cisalhamento, quando: (a) τ y z = 120M P a ; (b) τ y z = 55M P a ; (c) τ y z = 0 .